题目内容

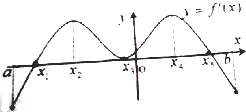
函数f（x）的定义域为开区间（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内的极值点是（　　）
分析：根据极值的定义，观察图象知导数值变化的个数，即为极值点的个数．
解答：解：因为图象是导函数的图象，所以导数值的符合代表函数单调性的变化．
由图象可知在x1处，左侧导数为负右侧为正，所以在x1处函数取得极小值．
在x5处，左侧导数为正右侧为负，所以在x1处函数取得极大值．
故选C．
点评：本题主要是通过导函数的图象研究函数的极值问题．如果是导函数，则需要看导数值的正负变化，如果是原函数，则看的是函数的单调性的变化．
练习册系列答案
相关题目
函数f（x）的定义域为{x|x≠0}，且满足对于定义域内任意的x1，x2都有等式f（x1•x2）=f（x1）+f（x2）
（Ⅰ）求f（1）的值；
（Ⅱ）判断f（x）的奇偶性并证明；
（Ⅲ）若f（2）=1，且f（x）在（0，+∞）上是增函数，解关于x的不等式f（2x-1）-3≤0．
若函数f（x）的定义域是[0，1），则F（x）=f[log 
12
(3-x)]的定义域为
 
．
已知a＞0且a≠1，函数f（x）=loga（x+1），g(x)=loga
11-x
，记F（x）=2f（x）+g（x）
（1）求函数F（x）的定义域D及其零点；
（2）试讨论函数F（x）在定义域D上的单调性；
（3）若关于x的方程F（x）-2m2+3m+5=0在区间[0，1）内仅有一解，求实数m的取值范围．
若函数f（x）的定义域为（-1，1），它在定义域内既是奇函数又是增函数，且f（a-3）+f（4-2a）＜0，则实数a的取值范围是（　　）
若函数f（x）的定义域为[-1，2]，则函数
f(x+2)
x
的定义域为（　　）
A、[-1，0）∪（0，2]
B、[-3，0）
C、[1，4]
D、（0，2]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网