题目内容
【题目】设单位向量 
对于任意实数λ都有| 
+ 
|≤| ﹣λ |成立，则向量 的夹角为（ ）
A.
B.
C.
D.
【答案】C
【解析】解：设单位向量 
的夹角为θ，
∵对于任意实数λ都有| 
+ 
|≤| ﹣λ |成立，
∴对于任意实数λ都有| + |2≤| ﹣λ |2成立，
即 
+ 
+| || |cosθ≤ +λ2 ﹣2λ| || |cosθ，
即1+ +cosθ≤1+λ2﹣2λcosθ，即λ2﹣2λcosθ﹣（ +cosθ）≥0恒成立，
∴△=4cos2θ+4（ +cosθ）≤0，整理可得（cosθ+ ）2≤0，
再由（cosθ+ ）2≥0可得（cosθ+ ）2=0，故cosθ=﹣ ，
∵θ∈[0，π]，∴θ= 
故选：C
【考点精析】掌握数量积表示两个向量的夹角是解答本题的根本，需要知道设
、
都是非零向量，
，
，
是与
的夹角，则
．
名校通行证有效作业系列答案
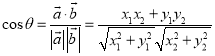【题目】某数学兴趣小组为了研究人的脚的大小与身高的关系，随机抽测了20位同学，得到如下数据：
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
身高 | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
脚长 | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
身高 | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
脚长 | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
（Ⅰ）请根据“序号为5的倍数”的几组数据，求出
关于
的线性回归方程；
（Ⅱ）若“身高大于175厘米”的为“高个”，“身高小于等于175厘米”的为“非高个”；“脚长大于42码”的为“大脚”，“脚长小于等于42码”的为“非大脚”.请根据上表数据完成
列联表，并根据列联表中数据说明能有多大的把握认为脚的大小与身高之间有关系.
附表及公式：
，
，
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
列联表：
高个 | 非高个 | 总计 | |
大脚 | |||
非大脚 | |||
总计 |
