题目内容
【题目】如图，已知抛物线
的焦点为
，直线
过
且依次交抛物线及圆
于点
四点，则
的最小值为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】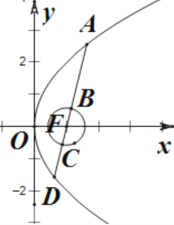
如图所示，抛物线
的焦点
，圆
的圆心坐标是
，半径
，设
，由抛物线的定义可知
， 
，显然直线
不可能平行于
轴，设直线
的方程为
代入到抛物线的方程中，得
， 
，显然
， 
，等号成立当且仅当
和
同时成立，即等号成立当且仅当
， 
的最小值是
，故选B.
【 方法点睛】本题主要考查抛物线的定义和几何性质，以及基本不等式求最值，属于难题. 与焦点、准线有关的问题一般情况下都与拋物线的定义有关，解决这类问题一定要注意点到点的距离与点到直线的距离的转化：（1）将抛线上的点到准线距转化为该点到焦点的距离；(2)将抛物线上的点到焦点的距离转化为到准线的距离，本题就是将
转化为到准线的距离后，再利用韦达定理与基本不等式使问题得到解决的.
练习册系列答案
相关题目
