题目内容
(本小题满分12分)已知函数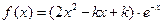 .
.
(1)当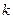 为何值时,
为何值时,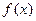 无极值;
无极值;
(2)试确定实数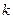 的值,使
的值,使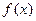 的极小值为
的极小值为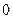 .
.
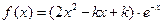 .
.(1)当
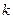 为何值时,
为何值时,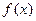 无极值;
无极值;(2)试确定实数
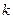 的值,使
的值,使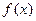 的极小值为
的极小值为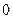 .
.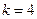 时,
时,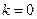 或
或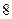 时,
时,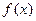 有极小值
有极小值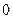
(1)∵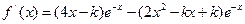
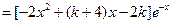
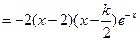
∴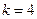 时,
时,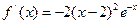 ≤
≤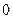 ,此时,
,此时,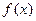 无极值.………… (5分)
无极值.………… (5分)
(2)当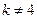 时,由
时,由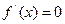 得
得 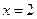 或
或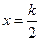 .
.
当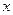 变化时,
变化时,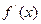 、
、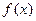 的变化如下表:
的变化如下表:
① 当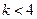 ,即
,即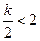 时
时
② 当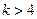 ,即
,即 时
时
∴ 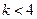 时,由
时,由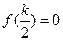 得
得 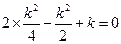 ,∴
,∴ 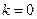
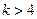 时,由
时,由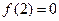 得
得 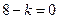 ,∴
,∴ 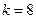
综上所述,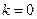 或
或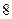 时,
时,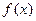 有极小值
有极小值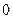 . …………………… (12分)
. …………………… (12分)
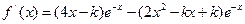
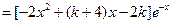
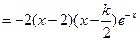
∴
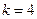 时,
时,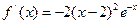 ≤
≤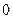 ,此时,
,此时,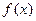 无极值.………… (5分)
无极值.………… (5分)(2)当
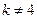 时,由
时,由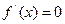 得
得 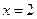 或
或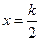 .
.当
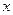 变化时,
变化时,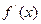 、
、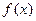 的变化如下表:
的变化如下表:① 当
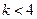 ,即
,即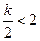 时
时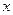 | 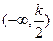 | 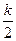 | 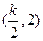 | 2 |  |
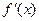 | 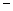 | 0 | 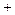 | 0 | 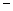 |
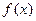 | 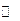 | 极小值 | 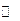 | 极大值 | 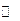 |
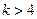 ,即
,即 时
时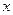 | 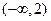 | 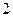 | 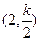 | 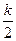 | 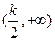 |
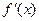 | 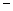 | 0 | 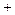 | 0 | 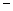 |
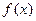 | 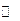 | 极小值 | 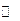 | 极大值 | 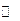 |
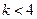 时,由
时,由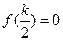 得
得 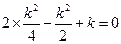 ,∴
,∴ 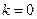
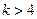 时,由
时,由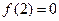 得
得 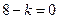 ,∴
,∴ 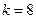
综上所述,
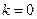 或
或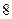 时,
时,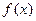 有极小值
有极小值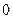 . …………………… (12分)
. …………………… (12分)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
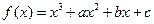 在
在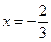 与
与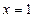 时都取得极值.
时都取得极值.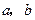 的值 (2)求函数
的值 (2)求函数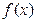 的单调区间;
的单调区间;  ,
,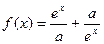 是
是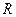 上的偶函数。
上的偶函数。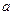 的值;
的值;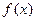 在
在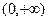 上是增函数
上是增函数
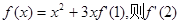 = ( )
= ( )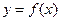 的图象与
的图象与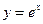 的图象关于直线
的图象关于直线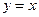 对称,则函数
对称,则函数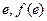 )处的切线方程为 .
)处的切线方程为 .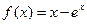 在点P处的切线平行于
在点P处的切线平行于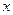 轴,且点P在
轴,且点P在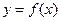 的图象上,则点P的坐标为 。
的图象上,则点P的坐标为 。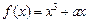 在
在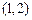 处的切线方程为 ▲ .
处的切线方程为 ▲ . 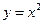 相切的直线方程为 .
相切的直线方程为 . 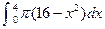 等于 ( )
等于 ( )