题目内容
如图,椭圆 (a>b>0)的上、下顶点分别为A、B,已知点B在直线l:
(a>b>0)的上、下顶点分别为A、B,已知点B在直线l: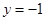 上,且椭圆的离心率e =
上,且椭圆的离心率e =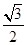 .
.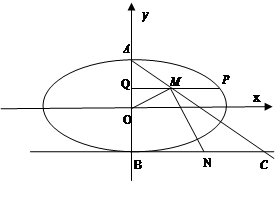
(1)求椭圆的标准方程;
(2)设P是椭圆上异于A、B的任意一点,PQ⊥y轴,Q为垂足,M为线段PQ中点,直线AM交直线l于点C,N为线段BC的中点,求证:OM⊥MN.
(1)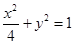 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)根据椭圆的性质,建立方程,即可求得;(2)可以设点P坐标,然后用点P的坐标表示M、N的坐标,进而可以表示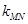 、
、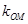 ,然后说明
,然后说明 即可.
即可.
试题解析:(1)依题意,得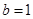 . ∵
. ∵ ,
,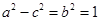 ,∴
,∴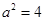 .
.
∴椭圆的标准方程为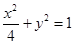
(2)证明:设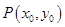 ,
,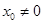 ,则
,则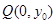 ,且
,且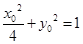 .∵
.∵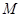 为线段
为线段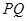 中点, ∴
中点, ∴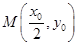 . 又
. 又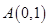 ,∴直线
,∴直线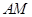 的方程为
的方程为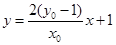 .
.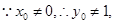 令
令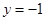 ,得
,得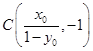 . 又
. 又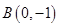 ,
,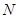 为线段
为线段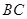 的中点,∴
的中点,∴ .
.
当 时,
时,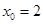 ,
,
此时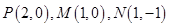 ,
,
∴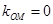 ,
,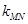 不存在,∴
不存在,∴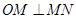 .
.
当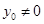 时,
时,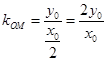 ,
, ,
,
∵ ,∴
,∴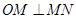
综上得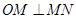 .
.
考点:(1)椭圆的标准方程;(2)两条直线垂直的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
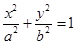 (a>b>0),过点(0,1),且离心率为
(a>b>0),过点(0,1),且离心率为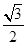 .
.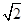 与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时,
与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时,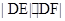 恒为定值.
恒为定值. 所围成的封闭图形的面积为
所围成的封闭图形的面积为 ,曲线C1上的点到原点O的最短距离为
,曲线C1上的点到原点O的最短距离为 .以曲线C1与坐标轴的交点为顶点的椭圆记为C2.
.以曲线C1与坐标轴的交点为顶点的椭圆记为C2.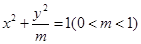 的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称.
的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称.
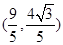 ,求m的值;
,求m的值;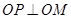 ,求m的取值范围.
,求m的取值范围.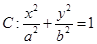
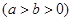 的左、右焦点分别
的左、右焦点分别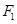 、
、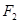 ,点
,点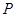 是椭圆短轴的一个端点,且焦距为6,
是椭圆短轴的一个端点,且焦距为6,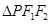 的周长为16.
的周长为16. 的方程;
的方程;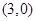 且斜率为
且斜率为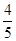 的直线
的直线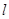 被椭圆
被椭圆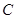 :
: 的离心率为
的离心率为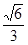 ,右焦点为(
,右焦点为( ,0).
,0).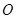 作两条互相垂直的射线,与椭圆交于
作两条互相垂直的射线,与椭圆交于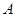 ,
,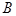 两点,求证:点
两点,求证:点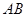 的距离为定值.
的距离为定值.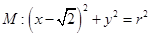
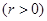 ,若椭圆
,若椭圆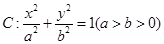 的右顶点为圆
的右顶点为圆 的圆心,离心率为
的圆心,离心率为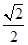 .
.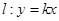 ,使得直线
,使得直线 与椭圆
与椭圆 分别交于
分别交于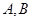 两点,与圆
两点,与圆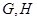 两点,点
两点,点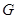 在线段
在线段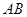 上,且
上,且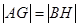 ,求圆
,求圆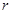 的取值范围.
的取值范围.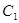 以双曲线
以双曲线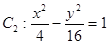 的实轴为短轴、虚轴为长轴,且与抛物线
的实轴为短轴、虚轴为长轴,且与抛物线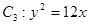 交于
交于 两点.
两点.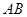 的长;
的长; 图像的公共区域内,是否存在一点
图像的公共区域内,是否存在一点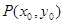 ,使得
,使得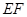 与
与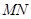 相互垂直平分于点
相互垂直平分于点 ?若存在,求点
?若存在,求点