题目内容
球放在墙角（两墙面，地面分别两两垂直），紧靠墙面和底面，球心到墙角顶点的距离是
，则球的体积是 ．（半径为R的球体积公式：V=
πR3）
【答案】分析：设球的半径为R，当球放在墙角时，同时与两墙面和地面相切可知球心与墙角顶点可构成边长为R的正方体，则正方体对角线即为球心到墙角顶点的距离，由此求出球的半径，可得球的体积．
解答：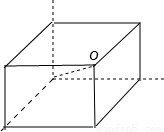
解：根据题意可知球心与墙角顶点可构成边长为a的正方体
则球心到墙角顶点的距离为正方体的对角线即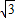
R
即
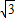R=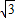
解得：R=1
故球的体积V=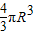
=
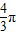
故答案为：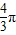
点评：本题主要考查了空间两点的距离，以及利用构造正方体进行解题，属于基础题．
解答：
解：根据题意可知球心与墙角顶点可构成边长为a的正方体则球心到墙角顶点的距离为正方体的对角线即
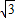R即
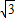R=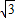解得：R=1
故球的体积V=
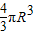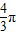
=故答案为：
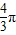
点评：本题主要考查了空间两点的距离，以及利用构造正方体进行解题，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
，则球的体积是 ．（半径为R的球体积公式：
）