题目内容
已知曲线C1的极坐标方程为ρ2cos2θ=8,曲线C2的极坐标方程为θ=
,曲线C1、C2相交于A、B两点.(p∈R)
(Ⅰ)求A、B两点的极坐标;
(Ⅱ)曲线C1与直线
(t为参数)分别相交于M,N两点,求线段MN的长度.
| π |
| 6 |
(Ⅰ)求A、B两点的极坐标;
(Ⅱ)曲线C1与直线
|
(Ⅰ)由
得:ρ2cos
=8,
∴ρ2=16,
即ρ=±4.
∴A、B两点的极坐标为:A(4,
),B(-4,
)或B(4,
).
(Ⅱ)由曲线C1的极坐标方程ρ2cos2θ=8化为ρ2(cos2θ-sin2θ)=8,
得到普通方程为x2-y2=8.
将直线
代入x2-y2=8,
整理得t2+2
t-14=0.
∴|MN|=
=2
.
|
| π |
| 3 |
∴ρ2=16,
即ρ=±4.
∴A、B两点的极坐标为:A(4,
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
(Ⅱ)由曲线C1的极坐标方程ρ2cos2θ=8化为ρ2(cos2θ-sin2θ)=8,
得到普通方程为x2-y2=8.
将直线
|
整理得t2+2
| 3 |
∴|MN|=
| ||||
| 1 |
| 17 |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
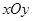 中,已知曲线
中,已知曲线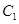 :
: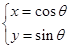 (
(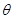 为参数),将
为参数),将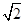 和
和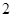 倍后得到曲线
倍后得到曲线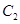 .以平面直角坐标系
.以平面直角坐标系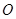 为极点,
为极点,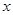 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线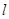 :
: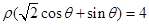 .
.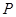 ,使点
,使点 中,已知曲线
中,已知曲线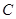 的参数方程是
的参数方程是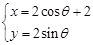 (
(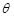 是参数),若以
是参数),若以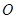 为极点,
为极点,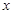 轴的正半轴为极轴,则曲线
轴的正半轴为极轴,则曲线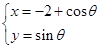 (
(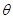 为参数,
为参数,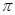 ))上任意一点,则
))上任意一点,则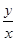 的取值范围是 。
的取值范围是 。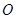 为原点,
为原点,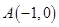 ,
,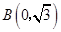 ,
,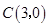 ,动点
,动点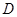 满足
满足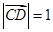 ,
,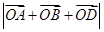 的取值范围是( )
的取值范围是( )
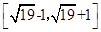
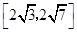
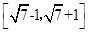
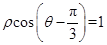 ,M,N分别为曲线C与x轴、y轴的交点.
,M,N分别为曲线C与x轴、y轴的交点.