题目内容
如图,已知平面A1B1C1平行于三棱锥V-ABC的底面,等边三角形AB1C所在平面与面ABC垂直,且∠ACB=90°,设AC=2a,BC=a.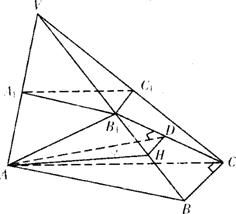
(Ⅰ)证明:B1C1为异面直线AB1与A1C1的公垂线;
(Ⅱ)求点A与平面VBC的距离;
(Ⅲ)求二面角A-VB-C的大小.
答案:方法1:传统的立体几何演绎法
(Ⅰ)证明:∵平面A1B1C1∥平面ABC,
∴B1C1∥BC,A1C1∥AC
∵BC⊥AC,∴B1C1⊥A1C1
又∵平面AB1C⊥平面ABC,平面AB1C∩平面
ABC=AC,
∴BC⊥平面AB1C,∴BC⊥AB,∴B1C1⊥AB1,
又∵A1C1∩B1C1=C1,B1C1∩AB1=B1.
∴B1C1为AB1与A1C1的公垂线.
(Ⅱ)解法1:过4作AD⊥B1C于D.
∵△AB1C为正三角形,∴D为B1C的中点.
∵BC上平面AB1C,∴BC⊥AD,
又B1C∩BC=C,∴AD⊥平面VBC,
∴线段AD的长即为点A到平面VBC的距离.
在正△AB1C中,AD=![]() ,AC=
,AC=![]() ×2a=
×2a=![]() a.
a.
∴点A到平面VBC的距离![]() a.
a.

解法2:取AC中点O连接B1O,则B1O⊥平面ABC,且B1O=![]() a.
a.
由(Ⅰ)知BC⊥B1C,设A到平面VBC的距离为x,
∴![]() ,
,
即![]() BC·AC·B1O=
BC·AC·B1O=![]() BC·B1C·x,解得
BC·B1C·x,解得
x=![]() a.
a.
即A到平面VBC的距离为![]() a.
a.
(Ⅲ)过D点作DH⊥VB于H,连AH,由三垂线定理知AH⊥VB
∴∠AHD是二面角A-VB-C的平面角.
在Rt△AHD中,
AD=![]() a·△B1DH=△B1BC·
a·△B1DH=△B1BC·![]() .
.
∴DH=![]() a.
a.
∴tan∠AHD=![]() .∴∠AHD=arctan
.∴∠AHD=arctan![]() .
.
所以,二面角A-VB-C的大小为arctan![]() .
.
方法2:空间向量法
取AC中点O,连接B1O,易知B1O⊥平面ABC,过O作直线0H∥BC交AB于H
取O为空间直角坐标系的原点,OH、OC、OB1所在
自线分别为x,y,z轴,如图建立空间直角坐标系,
则A(0,-a,0),B(a,a,0),C(0,a,0),B1(0,0,![]() a)
a)

(Ⅰ)![]() =(-a,0,0),
=(-a,0,0),![]() =(0,a,
=(0,a,![]() a),
a),
∴![]() ·
·![]() =(-a,0,0)·(0,a,
=(-a,0,0)·(0,a,![]() a)=0
a)=0
∴![]() ⊥
⊥![]() ,∴BC⊥AB1,
,∴BC⊥AB1,
又∵B1C1∥BC,由已知BC⊥AC,A1C1∥AC,
∴B1C1⊥A1C1,B1C1⊥AB1
即B1C1为AB1与A1C1的公垂线.
(Ⅱ)设n=(x,y,z)是平面佃C的一个法向量,
又![]() =(-a,0,0),
=(-a,0,0),![]() =(-a,-a,
=(-a,-a,![]() a),
a),
则
令z=![]() ,则x=0,y=3
,则x=0,y=3
∴n=(0,3,![]() )
)
设所求距离为d,d= a,
a,
∴点A到平在VBC的距离为![]() a.
a.
(Ⅲ)设平面VAB的一个法向量为m=(s,t,f),又![]() =(a,2a,0)
=(a,2a,0)
则
令f=![]() ,则s=6,t=-3
,则s=6,t=-3
即m=(6,-3,![]() ),
),
设二面角A-VB-C为α,n=(0,3,![]() )
)
cos<n,m>=![]()
又二面角A-VB-C为锐角,则二面角A-VB-C的大小为arccos![]() .
.

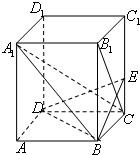 如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,
如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,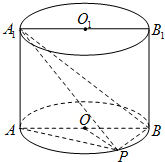 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°. 如图,已知正三棱柱ABC-A1B1C1,AA1=AB=2a,D、E分别为CC1、A1B的中点.
如图,已知正三棱柱ABC-A1B1C1,AA1=AB=2a,D、E分别为CC1、A1B的中点.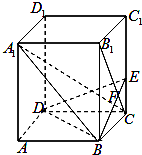 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F. 如图,已知棱长为1的正方体ABCD-A1B1C1D1.
如图,已知棱长为1的正方体ABCD-A1B1C1D1.