题目内容
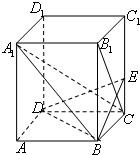 如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,
如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,过点B作B1C的垂线交侧棱CC1于点E.
(1)求证:面A1CB⊥平面BED;
(2)求A1B与平面BDE所成的角的正弦值
分析:(1)建立坐标系,写出两个平面上要用的点的坐标,构造两个向量,设出两个平面的法向量,根据向量垂直的充要条件得到两个平面的法向量,由于两个平面的法向量数量积为0,得到结论.
(2)本题要求的是线面角,写出线上的向量坐标,根据直线上的向量与平面的法向量所成的角的余弦的绝对值等于线面角的正弦值,得到结果.
(2)本题要求的是线面角,写出线上的向量坐标,根据直线上的向量与平面的法向量所成的角的余弦的绝对值等于线面角的正弦值,得到结果.
解答:解:以D为原点,DA,DC,DD1为坐标轴建立坐标系,设AB=1
由题意知A1(1,0,2),C(0,1,0),B(1,1,0),E(0,1,
),D(0,0,0)
∴
=(-1,1,-2),
=(-1,0,0),
=(0,1,
),
=(1,1,0)
(1)设面A1CB的法向量是
=(x,y,z),平面BED的法向量是
=(a,b,c)
根据法向量与平面的向量数量积是0
得到
=(0,2,1),
=(1,-1,2),
∴
•
=0,
∴面A1CB⊥平面BED.
(2)∵
=(0,1,-2)
平面BED的法向量是
=(1,-1,2),
设A1B与平面BDE所成的角为θ,
则sinθ=|cos<
,
>|=|
|=
,
∴A1B与平面BDE所成的角的正弦值为
.
由题意知A1(1,0,2),C(0,1,0),B(1,1,0),E(0,1,
| 1 |
| 2 |
∴
| A1C |
| BC |
| DE |
| 1 |
| 2 |
| DB |
(1)设面A1CB的法向量是
| m |
| n |
根据法向量与平面的向量数量积是0
得到
| m |
| n |
∴
| m |
| n |
∴面A1CB⊥平面BED.
(2)∵
| A1B |
平面BED的法向量是
| n |
设A1B与平面BDE所成的角为θ,
则sinθ=|cos<
| A1B |
| n |
| -5 | ||||
|
| ||
| 6 |
∴A1B与平面BDE所成的角的正弦值为
| ||
| 6 |
点评:本题是一个高考题型,空间向量与立体几何是近几年高考必考的内容,是一个送分题,题目的思维量不大,知识运算比较麻烦,同学们解题时要细心.

练习册系列答案
相关题目
 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.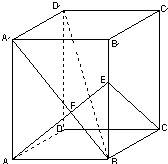 如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
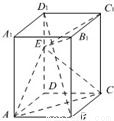 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.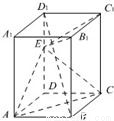 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.