题目内容
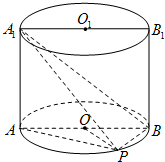 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.(1)求异面直线A1B与AP所成角的大小;(结果用反三角函数值表示)
(2)求点A到平面A1PB的距离.
分析:本题宜建立空间坐标系,用空间向量来解决求线面角证线线垂直,求点到面 距离.
(1)由题设条件,以O为原点,分别以OB,OO1为y,z轴的正向,并以AB的垂直平分线为x轴,建立空间直角坐标系,求出
与
的坐标,用公式求出线线角的余弦即得.
(2)用向量法求点到面的距离,先求出平面A1PB的法向量,再求线段对应的向量在面的法向量的投影的长度即可.
(1)由题设条件,以O为原点,分别以OB,OO1为y,z轴的正向,并以AB的垂直平分线为x轴,建立空间直角坐标系,求出
| A1B |
| AP |
(2)用向量法求点到面的距离,先求出平面A1PB的法向量,再求线段对应的向量在面的法向量的投影的长度即可.
解答:(1)解:以O为原点,分别以OB,OO1为y,z轴的正向,并以AB的垂直平分线为x轴,
建立空间直角坐标系.
由题意S表=2π•22+2π•2•AA1=20π,解得AA1=3.(2分)
易得相关点的坐标分别为:A(0,-2,0),P(
,1, 0),A1(0,-2,3),B(0,2,0).
得
=(
,3, 0),
=(0,4 , -3),(4分)
设
与
的夹角为θ,异面直线A1B与AP所成的角为α,
则cosθ=
=
>0,得α=θ=arc cos
,(6分)
即异面直线A1B与AP所成角的大小为arccos
.(7分)
(2)设平面A1PB的法向量为
=(u,v,w),则
⊥
,
⊥
∵
=(0,4,-3),
=(
,-1,0),
•
=0,
•
=0
∴
?
,(10分)
取v=3,得平面A1PB的一个法向量为
=(
,3,4),且|
|=2
,
=(0,0,-3)
所以点A到平面A1PB的距离d=
=
=
.(14分)
建立空间直角坐标系.
由题意S表=2π•22+2π•2•AA1=20π,解得AA1=3.(2分)
易得相关点的坐标分别为:A(0,-2,0),P(
| 3 |
得
| AP |
| 3 |
| A1B |
设
| A1B |
| AP |
则cosθ=
| ||||
|
|
2
| ||
| 5 |
2
| ||
| 5 |
即异面直线A1B与AP所成角的大小为arccos
2
| ||
| 5 |
(2)设平面A1PB的法向量为
| n |
| n |
| A1B |
| n |
| BP |
| A1B |
| BP |
| 3 |
| n |
| A1B |
| n |
| BP |
∴
|
|
取v=3,得平面A1PB的一个法向量为
| n |
| 3 |
| n |
| 7 |
| A1A |
所以点A到平面A1PB的距离d=
|
| ||||
|
|
| 12 | ||
2
|
| 6 |
| 7 |
| 7 |
点评:本考点是点、线、面间的距离计算、异面直线及其所成的角,本题宜建立空间坐标系,用空间向量来解决,故采用了向量法求点到面的距离,在做题时应根据题目的条件灵活选用解题的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
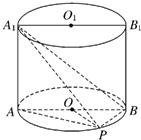 如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、圆O1的直径且A1A⊥平面PAB.
如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、圆O1的直径且A1A⊥平面PAB.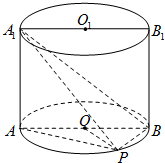 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为24π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为24π,OA=2,∠AOP=120°.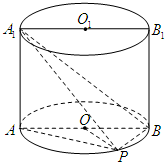 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,OA=2,∠AOP=120°,三棱锥A1-APB的体积为
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,OA=2,∠AOP=120°,三棱锥A1-APB的体积为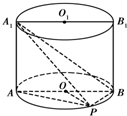 如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.
如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.