题目内容
【题目】如图,正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() ,点
,点![]() 为线段
为线段![]() 上一点.
上一点.
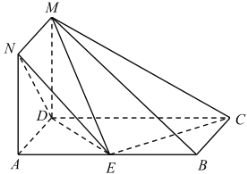
(1)若点![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的线面角的大小为
所成的线面角的大小为![]() ,求
,求![]() .
.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,由题意结合平面几何知识可得
,由题意结合平面几何知识可得![]() ,再由线面平行的判定即可得解;
,再由线面平行的判定即可得解;
(2)由题意结合面面垂直的性质、线面角的概念可得![]() ,进而可得
,进而可得![]() ,再由棱锥的体积公式求出
,再由棱锥的体积公式求出![]() 、
、![]() ,即可得解.
,即可得解.
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,如图:
,如图:
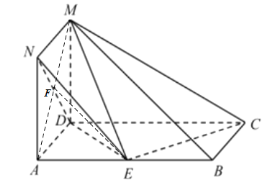
因为四边形![]() 为正方形,所以
为正方形,所以![]() 为线段
为线段![]() 的中点,
的中点,
又点![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)因为正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,
所以![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的线面角,所以
所成的线面角,所以![]() ,
,
因为![]() ,所以
,所以 ,
,![]() ,
,
所以![]() ,
,
因为四边形![]() 为正方形,四边形
为正方形,四边形![]() 为矩形,
为矩形,
由![]() 可得
可得![]() 平面
平面![]() ,
,
所以![]() ,
,
所以![]() .
.

【题目】“地摊经济”是李克强总理在本届政府工作报告中向全国人民发出的口号,某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() (
(![]() ,2,3,4,5,6),如表所示:
,2,3,4,5,6),如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量y(件) | q | 84 | 83 | 80 | 75 | 68 |
已知![]() ,
,![]() ,
,![]()
(1)试求q,若变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程![]() ;
;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数
称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式:线性回归方程中![]() ,
,![]() 的最小二乘估计分别为
的最小二乘估计分别为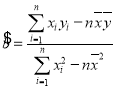 ,
,![]() )
)
【题目】(本小题满分12分)某商场为了了解顾客的购物信息,随机的在商场收集了100位顾客购物的相关数据,整理如下:
一次购物款(单位:元) | [0,50) | [50,100) | [100,150) | [150,200) | [200,+∞) |
顾客人数 | m | 20 | 30 | n | 10 |
统计结果显示100位顾客中购物款不低于100元的顾客占60%,据统计该商场每日大约有5000名顾客,为了增加商场销售额度,对一次性购物不低于100元的顾客发放纪念品(每人一件).(注:视频率为概率)
(1)试确定![]() 的值,并估计该商场每日应准备纪念品的数量;
的值,并估计该商场每日应准备纪念品的数量;
(2)为了迎接店庆,商场进行让利活动,一次购物款200元及以上的一次返利30元;一次性购物
款小于200元的按购物款的百分比返利,具体见下表:
一次购物款(单位:元) | [0,50) | [50,100) | [100,150) | [150,200) |
返利百分比 | 0 | 6% | 8% | 10% |
估计该商场日均让利多少元?