题目内容
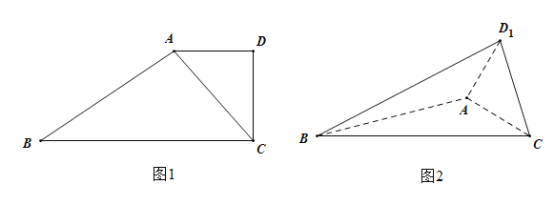
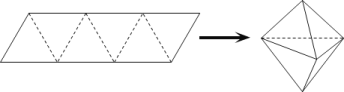
【题目】农历五月初五是端午节，民间有吃粽子的习惯，粽子又称粽籺，古称“角黍”，平行四边形形状的纸片是由六个边长为
的正三角形构成的，将它沿虚线折起来，可以得到如图所示粽子形状的六面体，则该六面体的体积为______；若该六面体内有一球，则该球表面积的最大值为______.
【答案】
【解析】
该六面体看成由两个全等的正四面体组合而成，正四面体的棱长为
，在棱长为的正四面体
中，其高为顶点
和底面
中心的连线段，易求；则该正四面体的体积易求，该六面体的体积可求. 当该六面体内有一球，且该球体积取最大值时，该球与
相切，过球心作
，则
就是球半径，利用等面积法可求半径，则球的表面积可求.
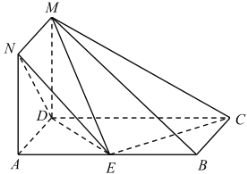
解：该六面体看成由两个全等的正四面体组合而成，正四面体的棱长为，如图，
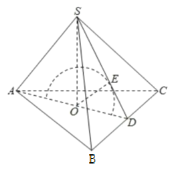
在棱长为的正四面体中，取
中点为
，连接，
，
作
平面
，垂足
在上，
则
，
，
，
则该正四面体的体积为
，
该六面体的体积
.
当该六面体内有一球，且该球体积取最大值时，球心为，
且该球与相切，过球心作，则就是球半径，
因为
，所以球半径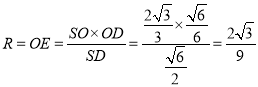
，
所以该球表面积的最大值为：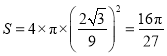
.
故答案为：；.
练习册系列答案
字词句段篇系列答案
相关题目
