题目内容
设函数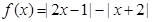
(1)求不等式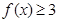 的解集;
的解集;
(2)若关于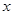 的不等式
的不等式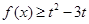 在
在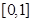 上无解,求实数
上无解,求实数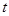 的取值范围
的取值范围
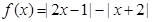
(1)求不等式
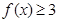 的解集;
的解集;(2)若关于
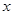 的不等式
的不等式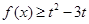 在
在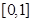 上无解,求实数
上无解,求实数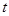 的取值范围
的取值范围(1)解集为 ;(2)
;(2) 或
或
 ;(2)
;(2) 或
或
试题分析:(1)该函数实质上是如下的一个分段函数,
 ,
, 所以原不等式转化为
 或
或 或
或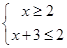 ,求出每个不等式的解,然后取并集即可
,求出每个不等式的解,然后取并集即可(2)关于
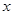 的不等式
的不等式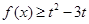 在
在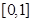 上无解,则
上无解,则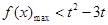 由上问可知函数在[0,1]单调递增,因此只要
由上问可知函数在[0,1]单调递增,因此只要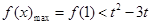 ,解此不等式即可
,解此不等式即可试题解析:(1)
 ,
, 所以原不等式转化为
 或
或 或
或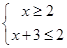 3分
3分解得
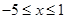 ,所以原不等式的解集为
,所以原不等式的解集为 6分
6分(2)由上问可知函数在[0,1]单调递增,因此只要
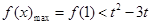 ,8分
,8分解得
 或
或 10分
10分
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 +
+ +
+ ≥a+b+c.
≥a+b+c. ≤9,则
≤9,则 的最大值是 .
的最大值是 . ,
, ,
, ,
, 中最大的是( )
中最大的是( )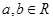 ,且
,且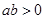 ,则下列不等式中,恒成立的是
,则下列不等式中,恒成立的是



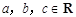 ,则下列说法正确的是 ( )
,则下列说法正确的是 ( )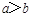 ,则
,则

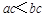 ,则
,则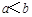

 和
和 是焦点相同且
是焦点相同且 的两个椭圆,有以下几个命题:①
的两个椭圆,有以下几个命题:① 一定没有公共点;②
一定没有公共点;② ;③
;③ ;④
;④ ,其中,所有真命题的序号为 。
,其中,所有真命题的序号为 。