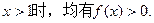题目内容
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[-1,1].
(1)求g(x)的解析式;
(2)判断g(x)的单调性.
(1)∵f(a+2)=18,f(x)=3x.
∴3a+2=18,即3a=2.
故g(x)=(3a)x-4x=2x-4x,x∈[-1,1].
(2)g(x)=-(2x)2+2x=-2+.
当x∈[-1,1]时,2x∈.令t=2x,
由二次函数单调性得
-2+在上是减函数,
∴函数g(x)在[-1,1]上是减函数.
解析

练习册系列答案
相关题目
(本小题8分)经过调查发现,某种新产品在投 放市场的30天中,前20天其价格直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
放市场的30天中,前20天其价格直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
| 时间 | 第4天 | 第12天 | 第20天 | 第28天 |
| 价格 (千元) | 34 | 42 | 50 | 34 |
(1)写出价格
 关于时间
关于时间 的函数表达式(
的函数表达式( 表示投放市场的第
表示投放市场的第 天)
天)(2)若销售量
 与时间
与时间 的函数关系式为
的函数关系式为 :
: ,问该产品投放市场第几天,日销售额最高?
,问该产品投放市场第几天,日销售额最高? 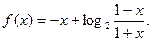
 的值;
的值; 在定义域内的单调性并给予证明.
在定义域内的单调性并给予证明.
 (
( )的图象与反比例函数
)的图象与反比例函数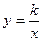 图象相交于点
图象相交于点 ,已知点
,已知点 的坐标为
的坐标为 ,点
,点 在第三象限内,且
在第三象限内,且 的面积为
的面积为 (
( 为坐标原点)
为坐标原点)
 的值;
的值; 轴的另一个交点为
轴的另一个交点为 ,
, 点为线段
点为线段
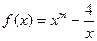 ,且
,且
 的值;
的值;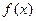 的奇偶性;
的奇偶性;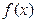 定义域为
定义域为 ,对于定义域内的任意x,y都有
,对于定义域内的任意x,y都有 ,且
,且 ,当
,当