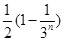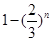题目内容
已知数列{ an }的通项公式为an =2n(n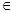 N*),把数列{an}的各项排列成如图所示的三角形数阵:
N*),把数列{an}的各项排列成如图所示的三角形数阵:
记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2 010对应于( )
| A.M(45,15) | B.M(45,25) |
| C.M(46,16) | D.M(46,25) |
A
解析试题分析:由数阵的排列规律知,数阵中的前n行共有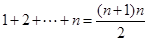
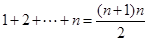 ,当n=44时,共有990项,又数阵中的偶数2 010是数列{an }的第1 005项,且
,当n=44时,共有990项,又数阵中的偶数2 010是数列{an }的第1 005项,且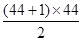 +15="1" 005,因此2010是数阵中第45行的第15个数故选A
+15="1" 005,因此2010是数阵中第45行的第15个数故选A
考点:数列的通项公式
点评:解决的关键是对于数阵的数字规律能结合等差数列的通项公式和求和来得到,属于基础题。

练习册系列答案
相关题目
已知数列{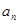 }满足
}满足 ,且
,且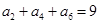 ,则
,则 的值是( )
的值是( )
A.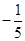 | B.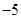 | C.5 | D.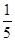 |
数列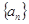 满足
满足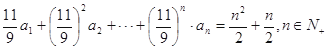 ,当
,当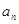 取最大值时,n= ( )
取最大值时,n= ( )
A.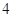 | B. | C.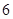 | D.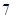 |
设等比数列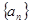 的公比为q,前n项和为
的公比为q,前n项和为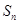 ,若
,若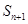 ,
,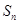 ,
,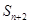 成等差数列,则公比q为( )
成等差数列,则公比q为( )
A.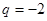 | B.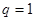 | C.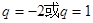 | D.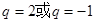 |
已知等比数列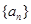 满足
满足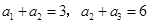 ,则
,则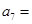 ( )
( )
| A.64 | B.81 | C.128 | D.243 |
若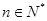 ,则1+2+22+23+…+2n-1=
,则1+2+22+23+…+2n-1=
| A.2n-1-1 | B.2n-1 | C.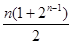 | D.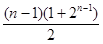 |
在正项等比数列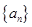 中,已知
中,已知 ,则
,则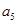 的值为( )
的值为( )
| A.8 | B.6 | C.4 | D.2 |
在等比数列{an}中,若a1a2a3=2,a2a3a4=16,则公比q= ( )
A. | B.2 | C.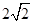 | D.8 |
 的首项、公比之和为1且首项是公比的2倍,那么它的前
的首项、公比之和为1且首项是公比的2倍,那么它的前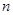 项的和为
项的和为