题目内容
函数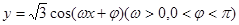 为奇函数,
为奇函数,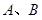 分别为函数图像上相邻的最高点与最低点,且
分别为函数图像上相邻的最高点与最低点,且 ,则该函数的一条对称轴为……………( ).
,则该函数的一条对称轴为……………( ).
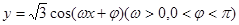 为奇函数,
为奇函数,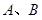 分别为函数图像上相邻的最高点与最低点,且
分别为函数图像上相邻的最高点与最低点,且 ,则该函数的一条对称轴为……………( ).
,则该函数的一条对称轴为……………( ). A.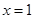 | B.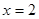 | C.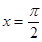 | D.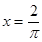 |
A
因为函数是奇函数,所以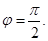 则
则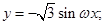 由条件知函数周期为
由条件知函数周期为
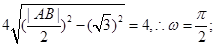 于是
于是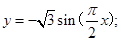 则该函数的对称轴为
则该函数的对称轴为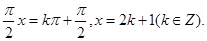 故选A
故选A
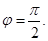 则
则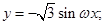 由条件知函数周期为
由条件知函数周期为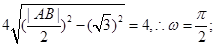 于是
于是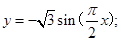 则该函数的对称轴为
则该函数的对称轴为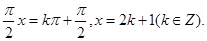 故选A
故选A
练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
题目内容
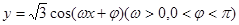 为奇函数,
为奇函数,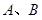 分别为函数图像上相邻的最高点与最低点,且
分别为函数图像上相邻的最高点与最低点,且 ,则该函数的一条对称轴为……………( ).
,则该函数的一条对称轴为……………( ). A.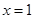 | B.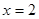 | C.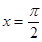 | D.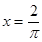 |
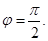 则
则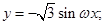 由条件知函数周期为
由条件知函数周期为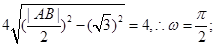 于是
于是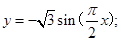 则该函数的对称轴为
则该函数的对称轴为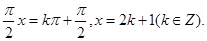 故选A
故选A
 走进文言文系列答案
走进文言文系列答案