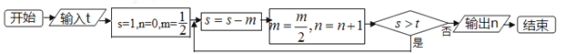题目内容
【题目】已知函数g(x)=ax2﹣2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|),x∈R;
(1)求实数a、b的值;
(2)若不等式 ![]() 对任意x∈R恒成立,求实数k的范围;
对任意x∈R恒成立,求实数k的范围;
(3)对于定义在[p,q]上的函数m(x),设x0=p,xn=q,用任意xi(i=1,2,…,n﹣1)将[p,q]划分成n个小区间,其中xi﹣1<xi<xi+1 , 若存在一个常数M>0,使得不等式|m(x0)﹣m(x1)|+|m(x1)﹣m(x2)|+…+|m(xn﹣1)﹣m(xn)|≤M恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试证明函数f(x)是在[1,3]上的有界变差函数,并求出M的最小值.
【答案】
(1)解:∵函数g(x)=ax2﹣2ax+1+b,
∵a>0,对称轴x=1,
∴g(x)在区间[2,3]上是增函数,
又∵函数g(x)故在区间[2,3]上的最大值为4,最小值为1,
∴ 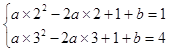 ,
,
解得:a=1,b=0.
∴g(x)=x2﹣2x+1
故实数a的值为1,b的值为0.
(2)解:由(1)可知g(x)=x2﹣2x+1,
∵f(x)=g(|x|),
∴f(x)=x2﹣2|x|+1,
∵ ![]() 对任意x∈R恒成立,
对任意x∈R恒成立,
令F(x)=f(x)+g(x)=x2﹣2x+1+x2﹣2|x|+1= 
根据二次函数的图象及性质可得F(x)min=f(1)=0
则F(x)min≥ ![]() 恒成立,即:
恒成立,即: ![]() ≤0
≤0
令log2k=t,
则有:t2﹣2t﹣3≤0,
解得:﹣1≤t≤3,
即 ![]() ,
,
得: ![]()
故得实数k的范围为 ![]()
(3)解:函数f(x)为[1,3]上的有界变差函数.
因为函数f(x)为[1,3]上的单调递增函数,且对任意划分T:1=x0<x1<…<xi<…<xn=3
有f(1)=f(x0)<f(x1)<…<f(xI)<…<f(xn)=f(3)
所以 ![]() |m(xi)﹣m(xi﹣1)|=f(x1)﹣f(x0)+f(x2)﹣f(x1)<…<f(xn)﹣f(xn﹣1)
|m(xi)﹣m(xi﹣1)|=f(x1)﹣f(x0)+f(x2)﹣f(x1)<…<f(xn)﹣f(xn﹣1)
=f(xn)﹣f(x0)=f(3)﹣f(1)=4恒成立,
所以存在常数M,使得 ![]() |m(xi)﹣m(xi﹣1)|≤M是恒成立.
|m(xi)﹣m(xi﹣1)|≤M是恒成立.
M的最小值为4,即Mmin=4
【解析】(1)由已知中g(x)在区间[2,3]的最大值为4,最小值为1,结合函数的单调性及最值,我们易构造出关于a,b的方程组,解得a,b的值;(2)求出f(x), ![]() 对任意x∈R恒成立等价于F(x)min=f(x)+g(x)恒成立,求实数k的范围;根据有界变差函数的定义,我们先将区间[1,3]进行划分,进而判断
对任意x∈R恒成立等价于F(x)min=f(x)+g(x)恒成立,求实数k的范围;根据有界变差函数的定义,我们先将区间[1,3]进行划分,进而判断 ![]() |m(xi)﹣m(xi﹣1)|≤M是否恒成立,进而得到结论.
|m(xi)﹣m(xi﹣1)|≤M是否恒成立,进而得到结论.
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值).

【题目】已知椭圆C1 , 抛物线C2焦点均在x轴上,C1的中心和C2顶点均为原点O,从每条曲线上各取两个点,将其坐标记录于表中,则C1的左焦点到C2的准线之间的距离为( )
x | 3 | ﹣2 | 4 |
|
y | -2 | 0 | ﹣4 |
|
A.![]() -1
-1
B.![]() -1
-1
C.1
D.2