题目内容
已知函数 (
(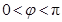 ,
, )为偶函数,且函数
)为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.
(1)求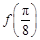 的值;
的值;
(2)将函数 的图象向右平移
的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数 的图象,求
的图象,求 的单调递减区间.
的单调递减区间.
 (
(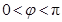 ,
, )为偶函数,且函数
)为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.(1)求
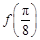 的值;
的值;(2)将函数
 的图象向右平移
的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数 的图象,求
的图象,求 的单调递减区间.
的单调递减区间.(1)  ;(2)
;(2)  .
.
 ;(2)
;(2)  .
.试题分析:(1)将原函数化简得
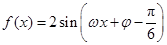 ,函数为偶函数,所以
,函数为偶函数,所以 得
得 ,由
,由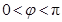 ,所以
,所以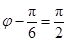 ,又图象的两相邻对称轴间的距离为
,又图象的两相邻对称轴间的距离为 ,所以周期
,所以周期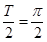 ,可得
,可得 ;(2)
;(2) 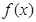 的图象向右平移
的图象向右平移 个单位后,得到
个单位后,得到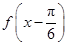 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到
的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到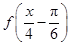 的图象,所以
的图象,所以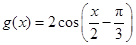 ,将
,将 看作整体,由余弦函数的性质,可得
看作整体,由余弦函数的性质,可得 的单调递减区间
的单调递减区间 .
.解:(1)


 .因为
.因为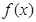 为偶函数,所以对
为偶函数,所以对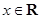 ,
, 恒成立,
恒成立,因此
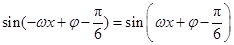 .
.即
 ,
,整理得
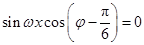 .因为
.因为 ,且
,且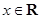 ,所以
,所以 .
.又因为
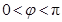 ,故
,故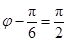 .所以
.所以 .
.由题意得
 ,所以
,所以 .故
.故 .
.因此
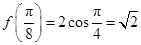 .
.(2)将
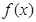 的图象向右平移
的图象向右平移 个单位后,得到
个单位后,得到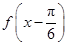 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到
的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到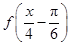 的图象.
的图象.所以
 .
.当
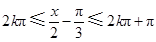 (
( ),
),即
 (
( )时,
)时, 单调递减,
单调递减,因此
 的单调递减区间为
的单调递减区间为 (
( ).
).
练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
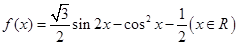
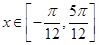 时,求函数
时,求函数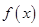 取得最大值和最小值时
取得最大值和最小值时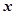 的值;
的值;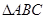 的内角A、B、C的对应边分别是
的内角A、B、C的对应边分别是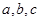 ,且
,且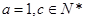 ,若向量
,若向量 与向量
与向量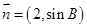 平行,求
平行,求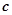 的值.
的值. 的图象沿
的图象沿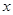 轴向左平移
轴向左平移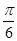 个单位后,得到一个关于
个单位后,得到一个关于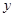 轴对称的图象,则
轴对称的图象,则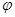
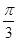
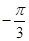
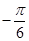
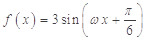 ,
,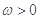 ,
,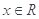 ,且以
,且以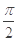 为最小正周期.
为最小正周期.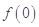 ;
;
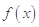 的解析式;
的解析式;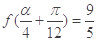 ,求
,求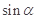 的值.
的值.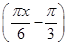 (0≤x≤9)的最大值与最小值之和为( )
(0≤x≤9)的最大值与最小值之和为( )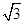
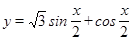 的图像,并说明这个图像是由
的图像,并说明这个图像是由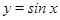 的图像经过怎样的变换得到的.
的图像经过怎样的变换得到的.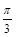 )的图象,只需把余弦曲线y=cosx上的所有的点 ( )
)的图象,只需把余弦曲线y=cosx上的所有的点 ( )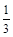 个单位长度
个单位长度 满足下了列哪些条件(填序号)__________.
满足下了列哪些条件(填序号)__________.
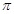 为最小周期;
为最小周期; 上单调递增;
上单调递增; 成中心对称.
成中心对称.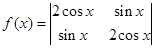 的最小正周期为 .
的最小正周期为 .