题目内容
如图：在平行四边形
中，
与
交于点
,设
= （ ）
A． | B． |
C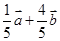． | D． |
A
解析试题分析：因为平行四边形中，与交于点，说明了点M是BC的三等份点，N是CD三等分点，那么根据，那么可知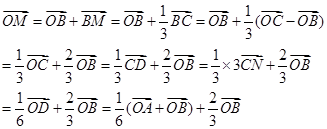
解得 可知为，选A.
考点：本题主要考查平面向量的基本定理的运用。
点评：解决该试题的关键是利用向量的加法和减法的几何意义，表述出所求解的向量，基本的原则就是确定出一组基底，然后用基底表示出向量即可。
练习册系列答案
手拉手全优练考卷系列答案
相关题目
已知平面向量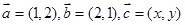
，且满足
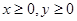。若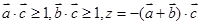
，则 （ ）
A． 有最大值-2 | B．z有最小值-2 | C．z有最大值-3 | D．z有最小值-3 |
已知|
|=2|
|≠0,且关于x的方程x2+||x+·=0有实根，则与的夹角的取值范围是
A． | B． | C． | D． |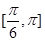
如图□ABCD中，
＝
，
＝
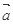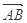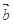则下列结论中正确的是 （ ）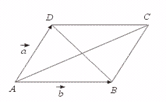
A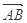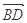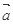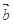．＋ ＝－ | B． ＋ ＝ |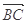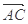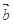
| C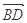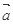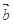．＝＋ | D．－ ＝＋ |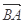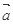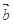
若
，则向量
的夹角为（ ）
A． | B． | C． | D． |
设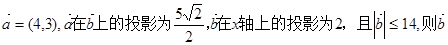
为（ ）
| A．(2，14) | B． | C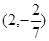． | D．(2，8) |
已知
是
内的一点，且
，
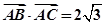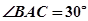，若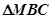
，
，
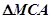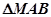的面积分别为
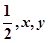，则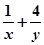
的最小值为（ ）
A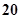． | B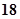． | C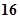． | D． |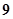
已知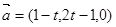
，
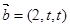，则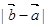
的最小值是（ ）
A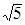． | B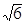． | C． | D．  |
已知向量
，则
等于（ ）
| A．5 | B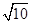． | C． | D．25 |