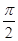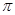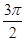题目内容
设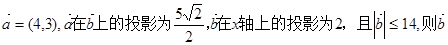 为( )
为( )
| A.(2,14) | B. | C.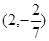 | D.(2,8) |
C
解析试题分析:设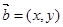 ,因为
,因为 在
在 轴上的投影是2,所以
轴上的投影是2,所以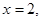 又因为
又因为 在
在 上的投影是
上的投影是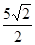 ,所以
,所以 与
与 的夹角余弦为
的夹角余弦为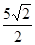 ,带入计算可得
,带入计算可得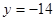 或
或 ,因为
,因为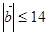 ,所以
,所以 .
.
考点:本小题主要考查向量的数量积、向量的投影和向量的夹角等概念和计算,考查学生的运算求解能力.
点评:向量的投影是一个数量,而不是向量.

练习册系列答案
相关题目
已知向量i=(1,0),j=(0,1),a=i-2j,b=i+λj,且a与b的夹角为锐角,则实数λ的取值范围( )
A.(-∞,-2)∪(-2, ) ) | B.(-∞,  ) ) |
C.(-2, ) ) | D.(-∞,-2) |
设向量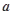 ,
, 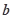 满足:
满足: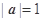 ,
, 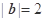 ,
,  , 则
, 则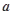 与
与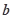 的夹角是( )
的夹角是( )
A.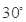 | B.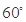 | C. | D.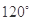 |
已知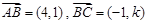 ,若A,B,C三点共线,则实数k的值为 ( )
,若A,B,C三点共线,则实数k的值为 ( )
A.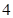 | B.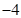 | C.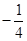 | D.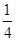 |
如图:在平行四边形 中,
中, 与
与 交于点
交于点
 ,设
,设
 = ( )
= ( )
A. | B. |
C.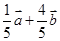 | D. |
向量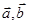 ,命题“若
,命题“若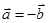 ,则
,则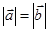 ”的逆命题是
”的逆命题是
A.若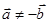 则 则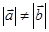 | B.若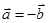 则 则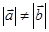 |
C.若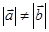 则 则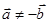 | D.若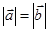 则 则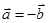 |
若等边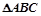 的边长为2,平面内一点M满足
的边长为2,平面内一点M满足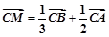 ,则
,则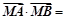 ( )
( )
A.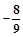 | B.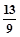 | C.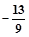 | D.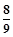 |
已知非零向量 、
、 满足向量
满足向量 与向量
与向量 的夹角为
的夹角为 ,那么下列结论中一定成立的是( )
,那么下列结论中一定成立的是( )
A. | B. | C. | D. // // |
 点的坐标是
点的坐标是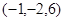 ,
, 点的坐标是
点的坐标是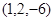 ,
, 为坐标原点,则向量
为坐标原点,则向量 与向量
与向量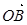 的夹角是( )
的夹角是( )