题目内容
5.下列命题:①求函数y=sin($\frac{π}{4}$-2x)的单调递减区间[kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$](k∈Z);
②终边在坐标轴上的角的集合是{a|a=$\frac{kπ}{2}$,k∈Z};
③若logm3<logn3<0,则0<m<n<1;
④函数f(x)=2sinx-1-a上有两个零点,则实数a的取值范围是[$\sqrt{3}$-1,1].
则所有错误命题的序号是③.
分析 直接求出函数的单调减区间判断①;写出终边在坐标轴上的角的集合判断②;由对数式的基本性质判断③;由三角函数的单调性结合函数的零点判定判断④.
解答 解:①∵y=sin($\frac{π}{4}$-2x)=-sin(2x-$\frac{π}{4}$),由$-\frac{π}{2}+2kπ≤2x-\frac{π}{4}≤\frac{π}{2}+2kπ$,解得:$-\frac{π}{8}+kπ≤x≤\frac{3π}{8}+2kπ,k∈Z$.
∴函数y=sin($\frac{π}{4}$-2x)的单调递减区间[kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$](k∈Z),①正确;
②终边在x轴上的角的集合为{a|a=kπ,k∈Z},终边在y轴上的角的集合为{a|a=$\frac{π}{2}+kπ$,k∈Z},
∴坐标轴上的角的集合是{a|a=kπ,k∈Z}∪{a|a=$\frac{π}{2}+kπ$,k∈Z}={a|a=$\frac{kπ}{2}$,k∈Z},②正确;
③若logm3<logn3<0,则0<n<m<1,③错误;
④∵当x$∈[\frac{π}{3},π]$时,t=sinx在区间[$\frac{π}{3}$,$\frac{π}{2}$]上为增函数,
在区间[$\frac{π}{2}$,π]上为减函数,且sin$\frac{π}{3}$=sin$\frac{2π}{3}$
∴当x∈$[\frac{π}{3},\frac{2π}{3}]$且x≠$\frac{π}{2}$时,存在两个自变量x对应同一个sinx
即当t∈[$\frac{\sqrt{3}}{2}$,1]时,方程t=sinx有两个零点
∵f(x)=2sinx-1-a在[$\frac{π}{3},π$]上有两个零点,即$\frac{1+a}{2}$=sinx在$[\frac{π}{3},π]$上有两个零点,
∴$\frac{1+a}{2}$∈[$\frac{\sqrt{3}}{2}$,1],解之得a∈[$\sqrt{3}$-1,1],④正确.
∴错误命题的序号是③.
故答案为:③.
点评 本题给出三角函数式,求满足函数在指定区间上有两个零点的参数a的取值范围.着重考查了三角函数的单调性与函数的图象与性质等知识,属于中档题.

| A. | k<-1 | B. | k>1 | C. | -1<k<1 | D. | k<-1或k>1 |
| A. | {x∈R|x+5=5} | B. | {x∈R|x+5>5} | C. | {x∈R|x2=0} | D. | {x∈R|x2+x+1=0} |
| A. | $\frac{3}{5}$ | B. | $±\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | ±$\frac{4}{5}$ |
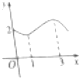 如图是偶函数y=f(x)的部分图象,根据图象所给的信息,有以下结论:
如图是偶函数y=f(x)的部分图象,根据图象所给的信息,有以下结论: