题目内容
设O是△ABC内部一点,且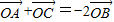 ,则△AOB与△AOC的面积之比为 .
,则△AOB与△AOC的面积之比为 .
【答案】分析:利用向量的运算法则:平行四边形法则得到O是AC边的中线的中点,得到三角形面积的关系.
解答:解:设AC的中点为D
∵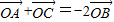
O为中线BD的中点
∴△AOB,△AOD,COD的面积相等
∴△AOB与△AOC的面积之比为1:2
故答案为1:2
点评:本题考查向量的运算法则:平行四边形法则及同底、同高的三角形面积相等.
解答:解:设AC的中点为D
∵
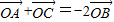
O为中线BD的中点
∴△AOB,△AOD,COD的面积相等
∴△AOB与△AOC的面积之比为1:2
故答案为1:2
点评:本题考查向量的运算法则:平行四边形法则及同底、同高的三角形面积相等.

练习册系列答案
相关题目
设O是△ABC内部一点,且
+
=-2
,则△AOB与△AOC的面积之比为( )
| OA |
| OC |
| OB |
| A、2:1 | B、1:2 |
| C、1:1 | D、2:5 |
设O是△ABC内部一点,且
+
=
,则△ABC与△AOC的面积之比为( )
| OA |
| OC |
| BO |
| A、3 | ||
B、
| ||
C、
| ||
D、
|