题目内容
已知向量 =
= ,
, =
= ,定义函数f(x)=
,定义函数f(x)= ·
· .
.
(1)求函数f(x)的表达式,并指出其最大值和最小值;
(2)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且f(A)=1,bc=8,求△ABC的面积S.
(1)f(x)=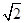 sin
sin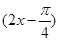 ,f(x)的最大值和最小值分别是
,f(x)的最大值和最小值分别是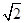 和-
和-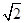 .(2)S=2
.(2)S=2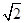 .
.
解析试题分析:(1)由向量的数量积公式及三角函数公式可得f(x) =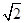 sin
sin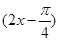 ,由此可得f(x)的最大值和最小值分别为
,由此可得f(x)的最大值和最小值分别为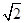 和-
和-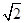 ;(2)由f(A)=1可求得角A,再由三角形面积公式S=
;(2)由f(A)=1可求得角A,再由三角形面积公式S= bcsin A即可得其面积.
bcsin A即可得其面积.
试题解析:(1)f(x) = =(-2sin x,-1)·(-cos x,cos 2x)
=(-2sin x,-1)·(-cos x,cos 2x)
=sin 2x-cos 2x=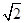 sin
sin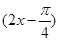 )
)
∴f(x)的最大值和最小值分别是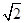 和-
和-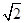
(2)∵f(A)=1,∴sin =
= .
.
∴2A- =
= 或2A-
或2A- =
=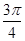 .∴A=
.∴A= 或A=
或A=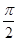 .
.
又∵△ABC为锐角三角形,∴A= .∵bc=8,
.∵bc=8,
∴△ABC的面积S= bcsin A=
bcsin A= ×8×
×8× =2
=2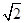
考点:1、三角函数及三角形的面积;2、向量的运算.

练习册系列答案
相关题目
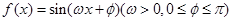 为偶函数,其图象上相邻的两个最低点间的距离为
为偶函数,其图象上相邻的两个最低点间的距离为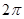 .
.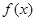 的解析式;
的解析式;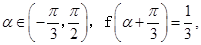 求
求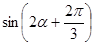 的值.
的值.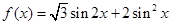 .
.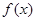 的最小正周期;
的最小正周期; 上的最大值和最小值.
上的最大值和最小值.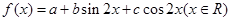 的图像过点
的图像过点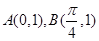 ,且b>0,又
,且b>0,又 的最大值为
的最大值为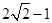 .
.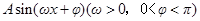 的形式;
的形式;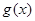 的图像?若能,请写出平移的过程;若不能,请说明理由.
的图像?若能,请写出平移的过程;若不能,请说明理由. ,设函数
,设函数 .
. ,且
,且 恰是函数f(x)在
恰是函数f(x)在 上的最大值,求A,b和三角形ABC的面积.
上的最大值,求A,b和三角形ABC的面积. cosx(x∈R).
cosx(x∈R). 的最小正周期为
的最小正周期为 .
. 时,求函数
时,求函数 的最小值;
的最小值; ,若
,若 ,且
,且 ,求
,求 的值.
的值. .
.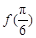 ;
;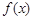 在
在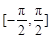 上的取值范围.
上的取值范围. ).
).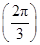 的值;
的值; 成立的x的取值集合.
成立的x的取值集合.