题目内容
(本小题满分12分)
已知数列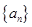 中,
中,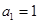 ,
,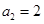 ,且
,且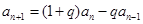
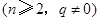 .
.
(1)设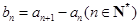 ,求
,求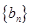 是的通项公式;
是的通项公式;
(2)求数列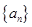 的通项公式;
的通项公式;
(3)若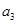 是
是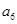 与
与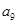 的等差中项,求
的等差中项,求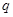 的值,并证明:对任意的
的值,并证明:对任意的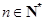 ,
,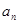 是
是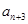 与
与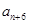 的等差中项.
的等差中项.
已知数列
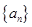 中,
中,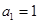 ,
,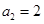 ,且
,且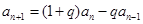
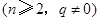 .
.(1)设
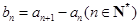 ,求
,求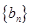 是的通项公式;
是的通项公式;(2)求数列
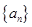 的通项公式;
的通项公式;(3)若
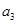 是
是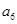 与
与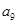 的等差中项,求
的等差中项,求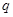 的值,并证明:对任意的
的值,并证明:对任意的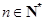 ,
,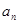 是
是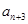 与
与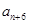 的等差中项.
的等差中项.(1)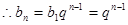
(2)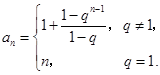
(3)证明三项构成等差中项的性质,只要利用等差中项的性质分析可得。
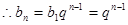
(2)
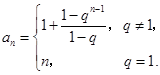
(3)证明三项构成等差中项的性质,只要利用等差中项的性质分析可得。
试题分析:(1)证明:由题
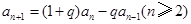 ,得
,得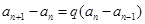 ,
, 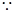
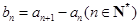 ,
,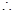
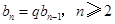 .又
.又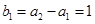 ,
,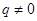 ,
, 所以
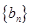 是首项为1,公比为
是首项为1,公比为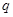 的等比数列.
的等比数列. 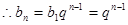
(2)解:由(Ⅰ),
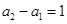 ,
,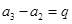 ,……,
,……,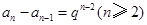 .
. 将以上各式相加,得
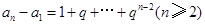 .
. 所以当
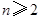 时,
时,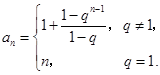
上式对
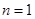 显然成立.
显然成立. (3)解:由(Ⅱ),当
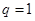 时,显然
时,显然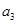 不是
不是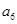 与
与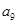 的等差中项,故
的等差中项,故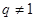 .
. 由
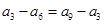 可得
可得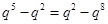 ,由
,由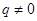 得
得 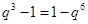 , ①
, ① 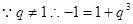 .于是
.于是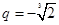 .
. 另一方面,
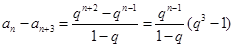 ,
,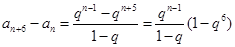 .
.由①可得
 .
.所以对任意的
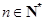 ,
,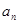 是
是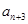 与
与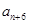 的等差中项.
的等差中项. 点评:解决的关键是对于数列的公式的熟练运用,等比数列和累加法思想的运用,属于中档题。易错点是对于公比的讨论容易忽略。

练习册系列答案
相关题目
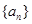 ,其前
,其前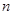 项和为
项和为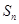 ,则点
,则点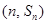 所在的抛物线可能为
所在的抛物线可能为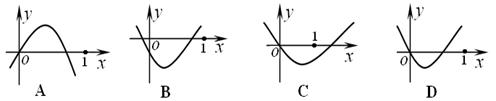
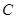 :
: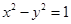 上的点
上的点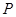 到点
到点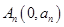 的距离的最小值为
的距离的最小值为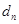 ,若
,若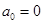 ,
,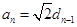 ,
,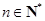
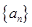 的通项公式;
的通项公式;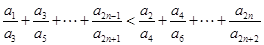 ;
;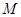 ,使得对
,使得对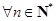 ,都有不等式:
,都有不等式: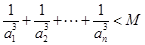 成立?请说明理由.
成立?请说明理由. 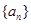 的各项均为正数,
的各项均为正数,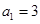 ,前
,前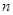 项和为
项和为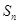 ,
,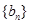 为等比数列,
为等比数列, 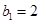 ,且
,且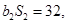
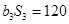 .
.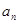 与
与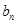 ;
;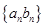 的前
的前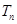 。
。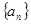 的前项
的前项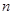 和为
和为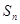 ,若
,若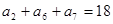 ,则
,则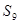 的值为( )
的值为( )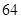
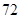
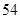
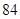
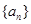 :1,4,7,……中,当
:1,4,7,……中,当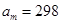 时,序号
时,序号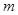 等于
等于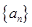 满足:
满足: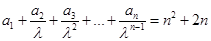 (其中常数
(其中常数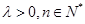 ).
).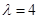 时,数列
时,数列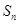 为数列
为数列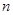 项和.求证:若任意
项和.求证:若任意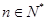 ,
,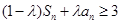
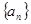 中,
中,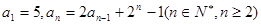 ,若存在实数
,若存在实数 ,使得数列
,使得数列 为等差数列,则
为等差数列,则