题目内容
(本小题12分)设函数y=x +ax
+ax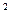 +bx+c的图像,如图所示,且与y=0在原点相切,若函数的极小值为–4,
+bx+c的图像,如图所示,且与y=0在原点相切,若函数的极小值为–4,
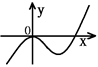
(1)求a、b、c的值;
(2)求函数的递减区间。
 +ax
+ax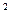 +bx+c的图像,如图所示,且与y=0在原点相切,若函数的极小值为–4,
+bx+c的图像,如图所示,且与y=0在原点相切,若函数的极小值为–4,
(1)求a、b、c的值;
(2)求函数的递减区间。
(1)-3 0 0
(2)函数的单调区间为(0,2)
解: (1)由图可知函数经过原点(0,0),代入函数得c=0-------------2分
(1)由图可知函数经过原点(0,0),代入函数得c=0-------------2分
导函数y =3x
=3x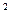 +2ax+b -----------------------4分
+2ax+b -----------------------4分
函数图像在原点处与x轴相切,则(0,0)在其导函数图像上,代入得b="0" ------6分
则y= x +ax
+ax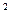 y
y =3x
=3x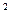 +2ax,令y
+2ax,令y =3x
=3x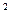 +2ax=0,得x=0或x=-
+2ax=0,得x=0或x=-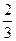 a
a
由图可知-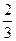 a>0 --------7分
a>0 --------7分
可知极小值为-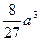 +
+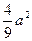 ,故-
,故-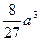 +
+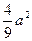 =-4,解得a=-3 ------10分
=-4,解得a=-3 ------10分
(2)由(1)a=-3,得y=x -3x
-3x
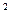 ,-
,-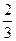 a="2"
a="2"
由上表显然函数的单调区间为(0,2)(或者表示为[0,2],区间开闭都行-----12分
 (1)由图可知函数经过原点(0,0),代入函数得c=0-------------2分
(1)由图可知函数经过原点(0,0),代入函数得c=0-------------2分导函数y
 =3x
=3x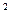 +2ax+b -----------------------4分
+2ax+b -----------------------4分函数图像在原点处与x轴相切,则(0,0)在其导函数图像上,代入得b="0" ------6分
则y= x
 +ax
+ax y
y =3x
=3x +2ax,令y
+2ax,令y =3x
=3x +2ax=0,得x=0或x=-
+2ax=0,得x=0或x=-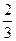 a
a由图可知-
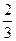 a>0 --------7分
a>0 --------7分| x | (-∞,0) | 0 | (0,-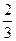 a) a) | -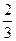 a a | (-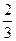 a,+∞) a,+∞) |
f (x) (x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值0 | ↘ | 极小值-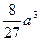 + +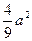 | ↗ |
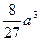 +
+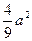 ,故-
,故-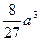 +
+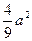 =-4,解得a=-3 ------10分
=-4,解得a=-3 ------10分(2)由(1)a=-3,得y=x
 -3x
-3x
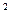 ,-
,-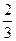 a="2"
a="2" 由上表显然函数的单调区间为(0,2)(或者表示为[0,2],区间开闭都行-----12分

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
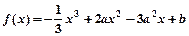
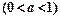
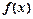 的单调区间、极值;
的单调区间、极值;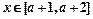 时,恒有
时,恒有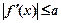 ,试确定
,试确定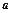 的取值范围。
的取值范围。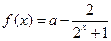 是奇函数
是奇函数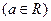 .
.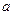 的值;
的值;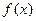 在(
在(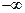 ,
,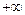 )上的单调性,并
)上的单调性,并 证明你的结论;
证明你的结论;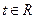 ,不
,不 等式
等式 恒成立,求实数
恒成立,求实数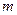 的取值范围.
的取值范围.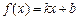 的图象与x、y轴分别相交于点A、 B,
的图象与x、y轴分别相交于点A、 B,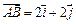 (
(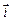 、
、 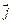 分别是与x、y轴正半轴同方向的单位向量), 函数
分别是与x、y轴正半轴同方向的单位向量), 函数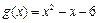
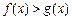 时,求函数
时,求函数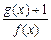 的最小值
的最小值 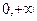 )上的单调性,并用定义证明.
)上的单调性,并用定义证明. 在区间
在区间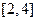 上是增函数,则实数
上是增函数,则实数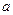 的取值范围是( )
的取值范围是( )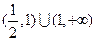
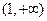
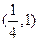
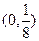

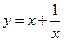 在
在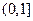 上是减函数,在
上是减函数,在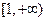 上是增函数;
上是增函数; 在
在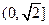 上是减函数,在
上是减函数,在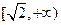 上是增函数;
上是增函数; 
 在
在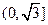 上是减函数,在
上是减函数,在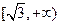 上是增函数;
上是增函数; 的值域是
的值域是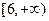 ,则实数
,则实数 的值是___________.
的值是___________.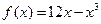 在区间
在区间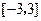 上的最小值是____.
上的最小值是____.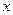 规定
规定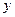 取
取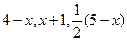 三个值中的最小值,则函数
三个值中的最小值,则函数