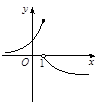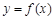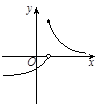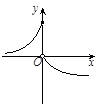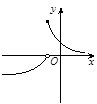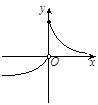题目内容
现有两个命题:
(1)若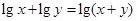 ,且不等式
,且不等式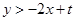 恒成立,则
恒成立,则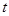 的取值范围是集合
的取值范围是集合 ;
;
(2)若函数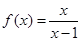 ,
,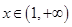 的图像与函数
的图像与函数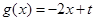 的图像没有交点,则
的图像没有交点,则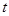 的取值范围是集合
的取值范围是集合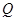 ;
;
则以下集合关系正确的是( )
A.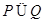 | B.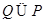 | C.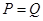 | D.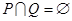 |
C
解析试题分析:法一、对(1):由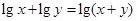 得
得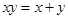 即
即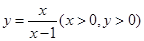 .
.
不等式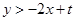 恒成立,等价于
恒成立,等价于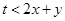 恒成立.这只需
恒成立.这只需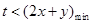 即可.
即可.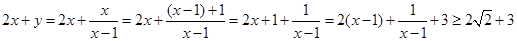 (当
(当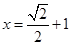 时,取等号).
时,取等号).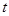 的取值范围是
的取值范围是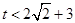 .
.
对(2):作出函数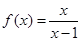 ,
,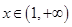 的图像与函数
的图像与函数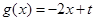 的图像如图所示:
的图像如图所示: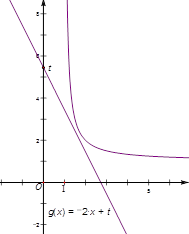
对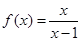 求导得:
求导得: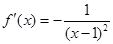 .由
.由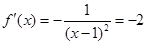 得
得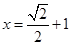 .由此得切点为
.由此得切点为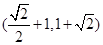 .代入
.代入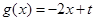 得
得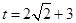 .由图可知
.由图可知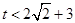 时,函数
时,函数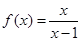 ,
,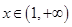 的图像与函数
的图像与函数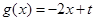 的图像没有交点,故
的图像没有交点,故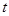 的取值范围为
的取值范围为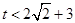 .
.
综上得: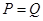 .所以选
.所以选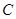 .
.
法二、对(1):由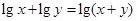 得
得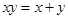 即
即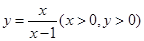 .
.
由于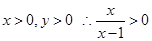 即
即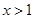 .
.
由此可以看出,这两个问题,实质上是同一个问题.所以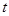 的取值范围相同.故选
的取值范围相同.故选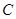 .
.
考点:1、对数运算;2、函数的图象;3、不等关系;4、重要不等式.

练习册系列答案
相关题目
已知函数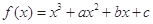 有两个极值点
有两个极值点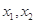 ,若
,若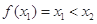 ,则关于
,则关于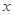 的方程
的方程 的不同实根个数为( )
的不同实根个数为( )
| A.3 | B.4 | C.5 | D.6 |
若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A.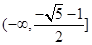 | B.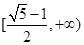 | C.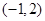 | D.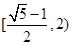 |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A. | B.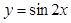 | C.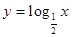 | D. |
若函数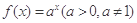 在
在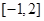 上的最大值为4,最小值为m,且函数
上的最大值为4,最小值为m,且函数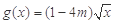 在
在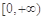 上是增函数,则a=( )
上是增函数,则a=( )
A.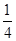 | B. | C.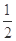 | D. |
已知定义在R上的函数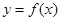 对任意的
对任意的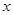 都满足
都满足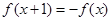 ,当
,当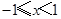
时,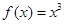 ,若函数
,若函数 至少6个零点,则
至少6个零点,则 的取值范围是( )
的取值范围是( )
A.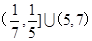 | B.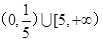 |
C. | D.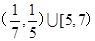 |
函数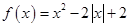 的定义域是
的定义域是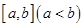 ,值域是
,值域是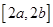 ,则符合条件的数组
,则符合条件的数组 的组数为( )
的组数为( )
A. | B.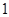 | C.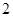 | D.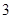 |
已知函数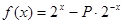 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.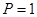 , , 为奇函数且为 为奇函数且为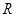 上的减函数 上的减函数 |
B.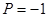 , , 为偶函数且为 为偶函数且为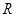 上的减函数 上的减函数 |
C.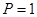 , , 为奇函数且为 为奇函数且为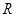 上的增函数 上的增函数 |
D.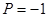 , , 为偶函数且为 为偶函数且为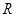 上的增函数 上的增函数 |
 的图象如图所示,则函数
的图象如图所示,则函数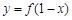 的大致图象是
的大致图象是