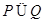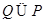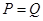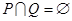题目内容
已知定义在R上的函数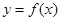 对任意的
对任意的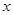 都满足
都满足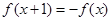 ,当
,当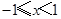
时,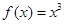 ,若函数
,若函数 至少6个零点,则
至少6个零点,则 的取值范围是( )
的取值范围是( )
A.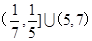 | B.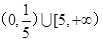 |
C. | D.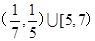 |
C
解析试题分析:函数g(x)=f(x)-loga|x|的零点个数,即函数y=f(x)与y=loga|x|的交点的个数;
由f(x+1)=-f(x),可得f(x+2)=f(x+1+1)=-f(x+1)=f(x),故函数f(x)是周期为2的周期函数,又由当-1≤x<1时,f(x)=x3,据此可以做出f(x)的图象,y=loga|x|是偶函数,当x>0时,y=logax,则当x<0时,y=loga(-x),做出y=loga|x|的图象: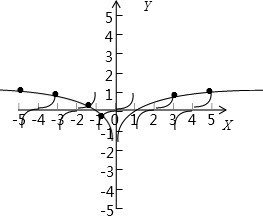
结合图象分析可得:要使函数y=f(x)与y=loga|x|至少有6个交点,则 loga5<1 或 loga5≥-1,解得 a>5,或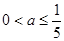 .故选C.
.故选C.
考点:1.考查函数图象的变化与运用

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
已知奇函数f(x)为R上的减函数,则关于a的不等式f(a2)+f(2a)>0的解集是 ( )
| A.(-2,0) | B.(0,2) |
| C.(-2,0)∪(0,2) | D.(-∞,-2)∪(0,+∞) |
下列函数中,既是偶函数又在区间(0,+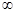 )上单调递减的是( )
)上单调递减的是( )
A.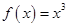 | B.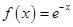 |
C.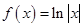 | D.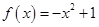 |
若偶函数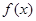 在
在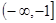 上是增函数,则下列关系式中成立的是( )
上是增函数,则下列关系式中成立的是( )
A.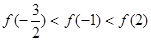 | B.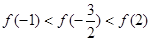 |
C.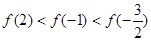 | D. |
下列说法,正确的是( )
A.对于函数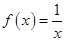 ,因为 ,因为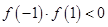 ,所以函数 ,所以函数 在区间 在区间 内必有零点 内必有零点 |
B.对于函数 ,因为 ,因为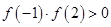 ,所以函数 ,所以函数 在区间 在区间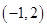 内没有零点 内没有零点 |
C.对于函数 ,因为 ,因为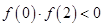 ,所以函数 ,所以函数 在区间 在区间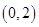 内必有零点 内必有零点 |
D.对于函数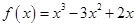 ,因为 ,因为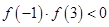 ,所以函数 ,所以函数 在区间 在区间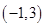 内有唯一零点 内有唯一零点 |
方程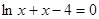 的解
的解 属于区间 ( )
属于区间 ( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
定义两种运算: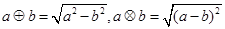 ,则函数
,则函数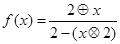 ( )
( )
| A.是奇函数 | B.是偶函数 |
| C.既是奇函数又是偶函数 | D.既不是奇函数又不是偶函数 |
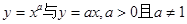 ,在同一直角坐标系第一象限中的图像可能是( )
,在同一直角坐标系第一象限中的图像可能是( )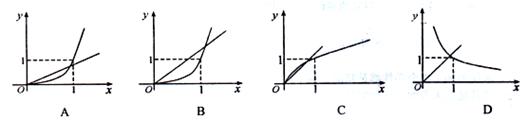
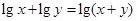 ,且不等式
,且不等式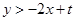 恒成立,则
恒成立,则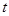 的取值范围是集合
的取值范围是集合 ;
;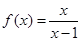 ,
,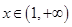 的图像与函数
的图像与函数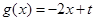 的图像没有交点,则
的图像没有交点,则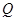 ;
;