题目内容
【题目】已知抛物线![]() :
: ![]() 的焦点
的焦点![]() 也是椭圆
也是椭圆![]() :
: ![]() (
(![]() )的一个焦点,
)的一个焦点, ![]() 与
与![]() 的公共弦长为
的公共弦长为![]() .
.
(Ⅰ)求![]() 的方程
的方程
(Ⅱ)过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
, ![]() 两点,与
两点,与![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,
, ![]() 同向.若
同向.若![]() 求直线
求直线![]() 的斜率;
的斜率;
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)由抛物线与椭圆共焦点可得![]() ,再由公共弦长可得公共点坐标
,再由公共弦长可得公共点坐标![]() 代入与前式联立可得
代入与前式联立可得![]() 的值;(Ⅱ)设
的值;(Ⅱ)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]()
与双曲线联立,利用韦达定理,将![]() 转化为关于
转化为关于![]() 的方程,解可得直线的斜率. 试题解析:解:(1)由抛物线
的方程,解可得直线的斜率. 试题解析:解:(1)由抛物线![]() :
: ![]() 的焦点
的焦点![]() ,所以
,所以![]() ,又由
,又由![]() 与
与![]() 的公共弦长为
的公共弦长为![]() ,得公共点坐标
,得公共点坐标![]() ,所以
,所以![]() ,解得
,解得![]() ,
, ![]() 得
得![]() :
: ![]()
(2)设![]() ,
, ![]() ,
, ![]() ,
, ![]()
由![]() ,得
,得![]() ,所以
,所以![]() ①
①
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]()
由![]() 得
得![]() ,
, ![]() ,
, ![]() ②
②
由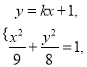 得
得![]() ,
, ![]() ,
, ![]() ③
③
将②③代入①,解得![]() .
.

【题目】一个单位有职工80人,其中业务人员56人,管理人员8人,服务人员16人,为了解职工的某种情况,决定采取分层抽样的方法。抽取一个容量为10的样本,每个管理人员被抽到的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 7 | 8 | 9 | 10 | 11 | 12 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据7至11月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,参考数据:
,参考数据: ![]() .
.
