题目内容
设函数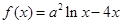 ,
,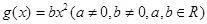 .
.
(1)当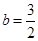 时,函数
时,函数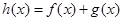 在
在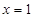 处有极小值,求函数
处有极小值,求函数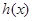 的单调递增区间;
的单调递增区间;
(2)若函数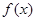 和
和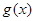 有相同的极大值,且函数
有相同的极大值,且函数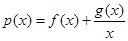 在区间
在区间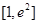 上的最大值为
上的最大值为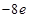 ,求实数
,求实数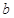 的值(其中
的值(其中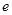 是自然对数的底数).
是自然对数的底数).
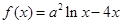 ,
,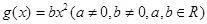 .
.(1)当
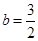 时,函数
时,函数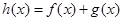 在
在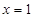 处有极小值,求函数
处有极小值,求函数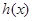 的单调递增区间;
的单调递增区间;(2)若函数
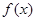 和
和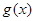 有相同的极大值,且函数
有相同的极大值,且函数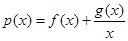 在区间
在区间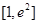 上的最大值为
上的最大值为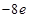 ,求实数
,求实数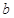 的值(其中
的值(其中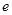 是自然对数的底数).
是自然对数的底数).(1)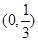 ,
,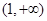 ;(2)
;(2)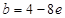 .
.
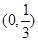 ,
,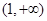 ;(2)
;(2)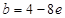 .
.试题分析:(1)先求
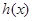 的导函数,利用极小值求未知数
的导函数,利用极小值求未知数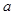 ,再利用导数判断单调性;(2)分别利用导数求
,再利用导数判断单调性;(2)分别利用导数求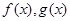 的极大值的关系式,再根据导数求
的极大值的关系式,再根据导数求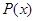 得最大值,得关系式(注意分情况讨论),综合以上关系求b的值.
得最大值,得关系式(注意分情况讨论),综合以上关系求b的值.试题解析:(1)
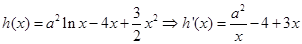 ,由题意
,由题意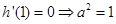
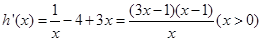
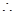 当
当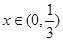 时,
时,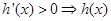 递增,当
递增,当 时,
时,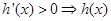 递增,
递增,
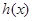 的递增区间为
的递增区间为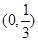 ,
,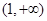 .
.(2)
 有极大值,则
有极大值,则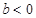 且
且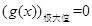 ,
,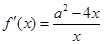 ,当
,当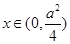 时,
时,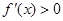 ,当
,当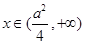 时,
时,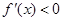 ,
,
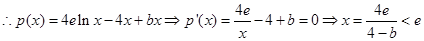
ⅰ)当
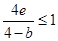 即
即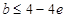 时,
时,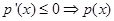 递减,
递减,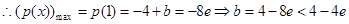 ,符合;
,符合;ⅱ)当
 即
即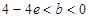 时,
时,当
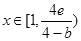 时,
时,
 递增,当
递增,当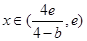 时,
时,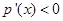
 递减,
递减,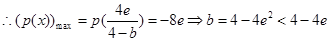 ,不符,舍去.
,不符,舍去.综上所述,
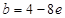 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作 ),
), (单位:弧度).
(单位:弧度).
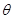 的函数;
的函数;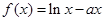 ,
,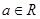 .
.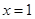 时,函数
时,函数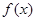 取得极值,求
取得极值,求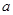 的值;
的值;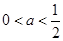 时,求函数
时,求函数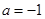 时,关于
时,关于 的方程
的方程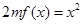
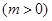 有唯一实数解,求实数
有唯一实数解,求实数 的值.
的值.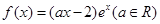 的一个极值点,
的一个极值点,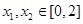 时,证明:
时,证明: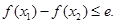
 ,则
,则 .
.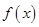 的定义域为
的定义域为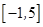 ,部分对应值如下表,
,部分对应值如下表, 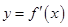 的图象如图所示.下列关于
的图象如图所示.下列关于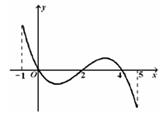
 ,
,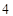 ;
;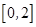 上是减函数;
上是减函数;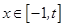 时,
时, 的最大值为4;
的最大值为4;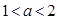 时,函数
时,函数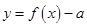 有
有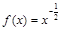 在点
在点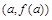 处的切线与两条坐标轴围成的三角形的面积为18,则
处的切线与两条坐标轴围成的三角形的面积为18,则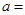 ( )
( ) ,若
,若 则
则 的值为( )
的值为( )


