题目内容
已知sin(π-α)= ,α∈(0,
,α∈(0, ).
).
(1)求sin2α-cos2 的值;
的值;
(2)求函数f(x)= cosαsin2x-
cosαsin2x- cos2x的单调递增区间.
cos2x的单调递增区间.
解:∵sin(π-α)= ,∴sinα=
,∴sinα= .
.
又∵α∈(0, ),∴cosα=
),∴cosα= .
.
(1)sin2α-cos2
=2sinαcosα-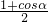
=2× ×
× -
-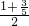 =
= .
.
(2)f(x)= ×
× sin2x-
sin2x- cos2x
cos2x
= sin(2x-
sin(2x- ).
).
令2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,
得kπ- ≤x≤kπ+
≤x≤kπ+ π,k∈Z.
π,k∈Z.
∴函数f(x)的单调递增区间为[kπ- ,kπ+
,kπ+ π],k∈Z.
π],k∈Z.
分析:通过条件求出sinα= ,cosα=
,cosα= ,
,
(1)利用二倍角的正弦,余弦的升角降次,直接求出sin2α-cos2 的值.
的值.
(2)化简函数f(x)= cosαsin2x-
cosαsin2x- cos2x为
cos2x为 sin(2x-
sin(2x- ),借助正弦函数的单调增区间,求出函数f(x)的单调递增区间.
),借助正弦函数的单调增区间,求出函数f(x)的单调递增区间.
点评:本题是基础题,考查二倍角格式的灵活应用,基本三角函数的单调增区间的求法,考查公式的灵活运用能力,基本知识的掌握程度.
 ,∴sinα=
,∴sinα= .
.又∵α∈(0,
 ),∴cosα=
),∴cosα= .
.(1)sin2α-cos2

=2sinαcosα-
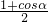
=2×
 ×
× -
-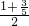 =
= .
.(2)f(x)=
 ×
× sin2x-
sin2x- cos2x
cos2x=
 sin(2x-
sin(2x- ).
).令2kπ-
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,得kπ-
 ≤x≤kπ+
≤x≤kπ+ π,k∈Z.
π,k∈Z.∴函数f(x)的单调递增区间为[kπ-
 ,kπ+
,kπ+ π],k∈Z.
π],k∈Z.分析:通过条件求出sinα=
 ,cosα=
,cosα= ,
,(1)利用二倍角的正弦,余弦的升角降次,直接求出sin2α-cos2
 的值.
的值.(2)化简函数f(x)=
 cosαsin2x-
cosαsin2x- cos2x为
cos2x为 sin(2x-
sin(2x- ),借助正弦函数的单调增区间,求出函数f(x)的单调递增区间.
),借助正弦函数的单调增区间,求出函数f(x)的单调递增区间.点评:本题是基础题,考查二倍角格式的灵活应用,基本三角函数的单调增区间的求法,考查公式的灵活运用能力,基本知识的掌握程度.

练习册系列答案
相关题目