题目内容
5.在空间坐标系中,设正四面体ABCD的顶点在x轴上的坐标分别为1,2,3,5,则该正四面体的棱长为4.分析 设B,C,D都在xOy面上,则A(3,ya,za),B(1,yb,0),C(2,yc,0),D(5,yd,0),由此推导出yb=yd,从而能求出该正四面体的棱长.
解答 解:设B,C,D都在xOy面上,
则A(3,ya,za),B(1,yb,0),C(2,yc,0),D(5,yd,0),
∴由正四面体的性质,得:
$\left\{\begin{array}{l}{\sqrt{4+({y}_{a}-{y}_{b})^{2}}=\sqrt{1+({y}_{c}-{y}_{b})^{2}}}\\{\sqrt{4+({y}_{a}-{y}_{b})^{2}}=\sqrt{4+({y}_{a}-{y}_{d})^{2}}}\\{\sqrt{4+({y}_{a}-{y}_{b})^{2}}=\sqrt{1+({y}_{b}-{y}_{c})^{2}}}\\{\sqrt{4+({y}_{a}-{y}_{b})^{2}}=\sqrt{16+({y}_{b}-{y}_{d})^{2}}}\end{array}\right.$,
∴yb=yd,
∴|BD|=$\sqrt{(5-1)^{2}}$=4,
∴该正四面体的棱长为4.
故答案为:4.
点评 本题考查正四面体的棱长的求法,是基础题,解题时要认真审题,注意空间两点间距离公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
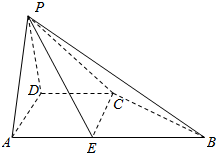 在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,PD=CD=AD=$\frac{1}{2}$AB,∠ADC=120°
在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,PD=CD=AD=$\frac{1}{2}$AB,∠ADC=120°
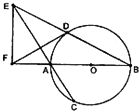 如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F. 如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.
如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.