Question

已知实数x，y满足条件

x-1≥0 x-y-1≤0，z=y-ax x-3y+3≥0

，若使z取得最大值的有序数对（x，y）有无数个，则a=

 

．

Answer 1

分析：先根据约束条件画出可行域，再利用几何意义求最值的方法，因为目标函数取得的最大值的最优解有无穷多个，所以必有目标函数所在的直线z=y-ax与三角形的某一边所在的直线重合，只需求出可行域边上所在直线的斜率即可．

解答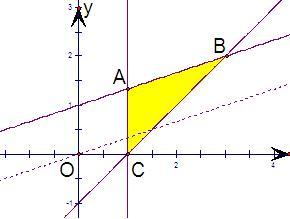：解：先根据约束条件画出可行域，
当直线线z=y-ax和直线AB重合时，
z取得最大值的有序数对（x，y）有无数个，
∴a=k_AB=

1

3

，
故填

1

3

．

点评：本题主要考查了简单的线性规划，以及利用几何意义求最值的方法反求参数的值，属于基础题．本题主要考查最优解的找法，以及两直线的位置关系．通过本题应进一步明确两点：①线性规划问题可能没有最优解；②当线性目标函数所表示的直线与可行域的某一条边界平行时，线性规划问题可以有无数个最优解．