题目内容
19．
如图，已知AB是圆O的直径，AB=4，EC是圆O的切线，切点为C，BC=1．过圆心O作BC的平行线，分别交EC和AC于D和点P，则OD=8．
分析 连接OC，确定OP⊥AC，OP=$\frac{1}{2}$BC=$\frac{1}{2}$，Rt△OCD中，由射影定理可得OC2=OP•OD，即可得出结论．
解答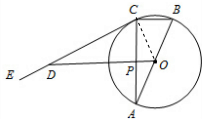 
解：连接OC，则OC⊥CD，
∵AB是圆O的直径，
∴BC⊥AC，
∵OP∥BC，
∴OP⊥AC，OP=$\frac{1}{2}$BC=$\frac{1}{2}$，
Rt△OCD中，由射影定理可得OC2=OP•OD，
∴4=$\frac{1}{2}$OD，
∴OD=8．
故答案为：8．
点评 本题考查圆的直径与切线的性质，考查射影定理，考查学生的计算能力，比较基础．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
9．设α，β是两个不同的平面，m是直线且m?α，“m∥β“是“α∥β”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
10．下列双曲线中，渐近线方程为y=±2x的是（ ）
| A． | x2-$\frac{y^2}{4}$=1 | B． | $\frac{x^2}{4}$-y2=1 | C． | x2-$\frac{y^2}{2}$=1 | D． | $\frac{x^2}{2}$-y2=1 |
如图，在⊙O中，相交于点E的两弦AB，CD的中点分别是M，N，直线MO与直线CD相交于点F，证明：
14．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{5}{4}$，且其右焦点为F2（5，0），则双曲线C的方程为（ ）
| A． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 | B． | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | C． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | D． | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 |
