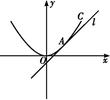
题目内容
已知F是椭圆C: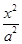 +
+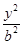 =1(a>b>0)的右焦点,点P在椭圆C上,线段PF与圆(x-
=1(a>b>0)的右焦点,点P在椭圆C上,线段PF与圆(x-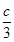 )2+y2=
)2+y2=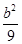 相切于点Q,且
相切于点Q,且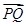 =2
=2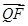 ,则椭圆C的离心率等于( )
,则椭圆C的离心率等于( )
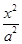 +
+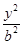 =1(a>b>0)的右焦点,点P在椭圆C上,线段PF与圆(x-
=1(a>b>0)的右焦点,点P在椭圆C上,线段PF与圆(x-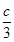 )2+y2=
)2+y2=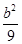 相切于点Q,且
相切于点Q,且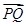 =2
=2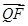 ,则椭圆C的离心率等于( )
,则椭圆C的离心率等于( )A.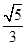 | B.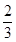 | C.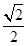 | D.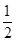 |
A
记椭圆的左焦点为F′,
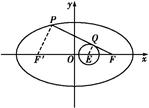
圆(x-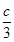 )2+y2=
)2+y2=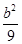 的圆心为E,
的圆心为E,
连接PF′、QE.
∵|EF|=|OF|-|OE|=c-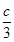 =
=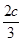 ,
,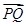 =2
=2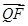 ,
,
∴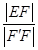 =
=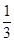 =
=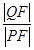 ,
,
∴PF′∥QE,
∴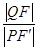 =
=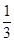 ,且PF′⊥PF.
,且PF′⊥PF.
又∵|QE|= (圆的半径长),
(圆的半径长),
∴|PF′|=b.
据椭圆的定义知:|PF′|+|PF|=2a,
∴|PF|=2a-b.
∵PF′⊥PF,
∴|PF′|2+|PF|2=|F′F|2,
∴b2+(2a-b)2=(2c)2,
∴2(a2-c2)+b2=2ab,
∴3b2=2ab,
∴b=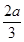 ,c=
,c=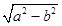 =
=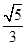 a,
a,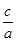 =
=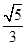 ,
,
∴椭圆的离心率为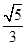 .
.

圆(x-
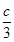 )2+y2=
)2+y2=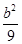 的圆心为E,
的圆心为E,连接PF′、QE.
∵|EF|=|OF|-|OE|=c-
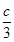 =
=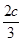 ,
,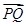 =2
=2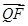 ,
,∴
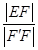 =
=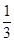 =
=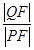 ,
,∴PF′∥QE,
∴
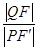 =
=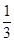 ,且PF′⊥PF.
,且PF′⊥PF.又∵|QE|=
 (圆的半径长),
(圆的半径长),∴|PF′|=b.
据椭圆的定义知:|PF′|+|PF|=2a,
∴|PF|=2a-b.
∵PF′⊥PF,
∴|PF′|2+|PF|2=|F′F|2,
∴b2+(2a-b)2=(2c)2,
∴2(a2-c2)+b2=2ab,
∴3b2=2ab,
∴b=
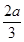 ,c=
,c=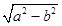 =
=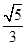 a,
a,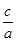 =
=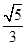 ,
,∴椭圆的离心率为
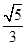 .
.
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
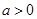 ,向量
,向量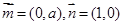 ,经过定点
,经过定点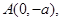 以
以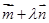 为方向向量的直线与经过定点
为方向向量的直线与经过定点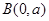 以
以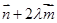 为方向向量的直线相交于
为方向向量的直线相交于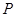 ,其中
,其中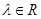 ,
,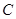 的方程;(2)若
的方程;(2)若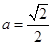 ,过
,过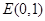 的直线交曲线
的直线交曲线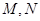 两点,求
两点,求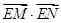 的取值范围。
的取值范围。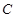 :
: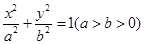 的离心率为
的离心率为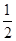 ,右焦点
,右焦点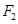 到直线
到直线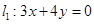 的距离为
的距离为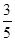 .
.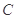 的方程;
的方程;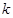 (
(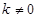 )的直线
)的直线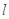 与椭圆
与椭圆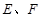 两点,
两点,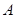 为椭圆的右顶点,直线
为椭圆的右顶点,直线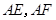 分别交直线
分别交直线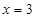 于点
于点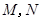 ,线段
,线段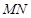 的中点为
的中点为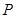 ,记直线
,记直线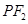 的斜率为
的斜率为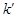 ,求证:
,求证: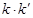 为定值.
为定值.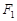 、
、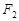 为双曲线
为双曲线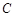 :
: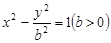 的左、右焦点,过
的左、右焦点,过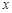 轴的直线,在
轴的直线,在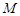 ,且
,且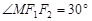 .圆
.圆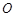 的方程是
的方程是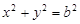 .
. 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为 、
、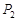 ,求
,求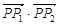 的值;
的值;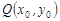 作圆
作圆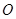 的切线
的切线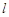 交双曲线
交双曲线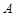 、
、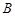 两点,
两点,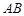 中点为
中点为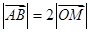 .
.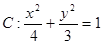 ,直线
,直线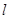 的方程为
的方程为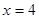 ,过右焦点
,过右焦点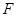 的直线
的直线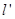 与椭圆交于异于左顶点
与椭圆交于异于左顶点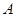 的
的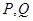 两点,直线
两点,直线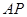 ,
,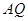 交直线
交直线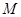 ,
,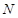 .
.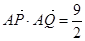 时,求此时直线
时,求此时直线
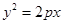 与直线
与直线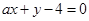 相交于A、B两点,其中A点的坐标是(1,2)。如果抛物线的焦点为F,那么
相交于A、B两点,其中A点的坐标是(1,2)。如果抛物线的焦点为F,那么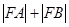 等于( )
等于( )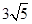 D.7
D.7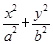 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=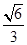 ,一条准线方程为x=
,一条准线方程为x=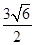
 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;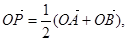 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆; 有相同的焦点;
有相同的焦点;  的距离与到定直线
的距离与到定直线 的距离相等的点的轨迹是抛物线.
的距离相等的点的轨迹是抛物线.