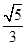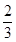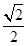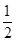题目内容
如图所示,直线l:y=x+b与抛物线C:x2=4y相切于点A.
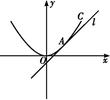
(1)求实数b的值;
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程.

(1)求实数b的值;
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程.
(1) b=-1 (2) (x-2)2+(y-1)2=4
解:(1)由
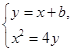 得x2-4x-4b=0.(*)
得x2-4x-4b=0.(*)因为直线l与抛物线C相切,
所以Δ=(-4)2-4×(-4b)=0,
解得b=-1.
(2)由(1)可知b=-1,故方程(*)即为x2-4x+4=0,
解得x=2.将其代入x2=4y,得y=1.
故点A(2,1).
因为圆A与抛物线C的准线相切,
所以圆A的半径r等于圆心A到抛物线的准线y=-1的距离,
即r=|1-(-1)|=2,
所以圆A的方程为(x-2)2+(y-1)2=4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
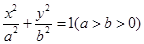 的右焦点为
的右焦点为 ,点
,点 在椭圆上.
在椭圆上.
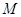 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过 ,
,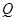 两点,问:△
两点,问:△ 的周长是否为定值?如果是,求出定值;如果不是,说明理由.
的周长是否为定值?如果是,求出定值;如果不是,说明理由. ,直线
,直线 是直线上的线段,且
是直线上的线段,且 是椭圆上一点,求
是椭圆上一点,求 面积的最小值。
面积的最小值。 x和y=-
x和y=-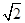 ,设O为坐标原点,动点P满足
,设O为坐标原点,动点P满足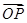 =
=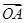 +
+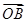 .
.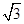 ,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点.
,0)作两条互相垂直的直线l1,l2,直线l1,l2与点P的轨迹的相交弦分别为CD,EF,设CD,EF的弦中点分别为M,N,求证:直线MN恒过一个定点. +
+ =1(a>b>0)交于A(x1,y1),B(x2,y2)两点,已知m=(ax1,by1),n=(ax2,by2),若m⊥n且椭圆的离心离e=
=1(a>b>0)交于A(x1,y1),B(x2,y2)两点,已知m=(ax1,by1),n=(ax2,by2),若m⊥n且椭圆的离心离e= ,又椭圆经过点(
,又椭圆经过点(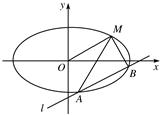
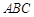 的两个顶点
的两个顶点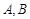 的坐标分别是
的坐标分别是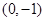 ,
,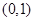 ,且
,且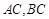 所在直线的斜率之积等于
所在直线的斜率之积等于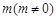 .
.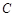 的轨迹
的轨迹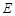 的方程,并判断轨迹
的方程,并判断轨迹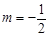 时,过点
时,过点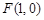 的直线
的直线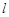 交曲线
交曲线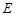 于
于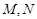 两点,设点
两点,设点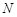 关于
关于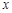 轴的对称点为
轴的对称点为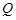 (
(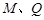 不重合), 试问:直线
不重合), 试问:直线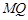 与
与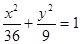 的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
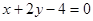
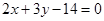

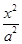 +
+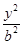 =1(a>b>0)的右焦点,点P在椭圆C上,线段PF与圆(x-
=1(a>b>0)的右焦点,点P在椭圆C上,线段PF与圆(x-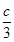 )2+y2=
)2+y2=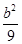 相切于点Q,且
相切于点Q,且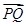 =2
=2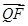 ,则椭圆C的离心率等于( )
,则椭圆C的离心率等于( )