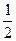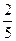题目内容
(13分)在某次抽奖活动中,一个口袋里装有5个白球和5个黑球,所有球除颜色外无任何不同,每次从中摸出2个球,观察颜色后放回,若为同色,则中奖。
(Ⅰ)求仅一次摸球中奖的概率;
(Ⅱ)求连续2次摸球,恰有一次不中奖的概率;
(Ⅲ)记连续3次摸球中奖的次数为 ,求
,求 的分布列。
的分布列。
(Ⅰ)求仅一次摸球中奖的概率;
(Ⅱ)求连续2次摸球,恰有一次不中奖的概率;
(Ⅲ)记连续3次摸球中奖的次数为
 ,求
,求 的分布列。
的分布列。(1)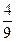 (2)
(2)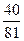 (3)
(3) 的分布列如下表
的分布列如下表
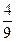 (2)
(2)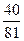 (3)
(3) 的分布列如下表
的分布列如下表 | 0 | 1 | 2 | 3 |
| P | 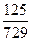 | 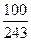 | 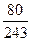 |  |
(Ⅰ)设仅一次摸球中奖的 概率为P1,则P1=
概率为P1,则P1=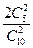 =
=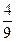 ……………………3分
……………………3分
(Ⅱ)设连续2次摸球(每次摸后放回),恰有一次不中奖的概率为P2,则
P2=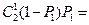
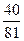 ………………………………………………7分
………………………………………………7分
(Ⅲ) 的取值可以是0,1,2,3
的取值可以是0,1,2,3
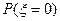 =(1-
=(1-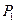 )3=
)3=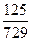 ,
,
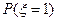 =
=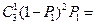
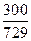 =
=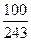 ,
,
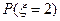 =
=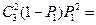 =
=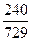 =
=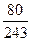 ,
,
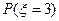 =
=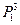 =
=
所以 的分布列如下表
的分布列如下表
………………………………………………………13分
 概率为P1,则P1=
概率为P1,则P1=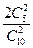 =
=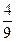 ……………………3分
……………………3分(Ⅱ)设连续2次摸球(每次摸后放回),恰有一次不中奖的概率为P2,则
P2=
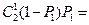
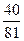 ………………………………………………7分
………………………………………………7分(Ⅲ)
 的取值可以是0,1,2,3
的取值可以是0,1,2,3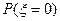 =(1-
=(1-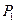 )3=
)3=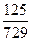 ,
,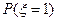 =
=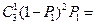
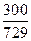 =
=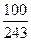 ,
,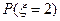 =
=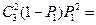 =
=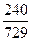 =
=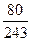 ,
,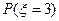 =
=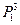 =
=
所以
 的分布列如下表
的分布列如下表 | 0 | 1 | 2 | 3 |
| P | 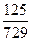 | 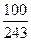 | 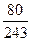 |  |

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
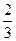 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为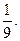
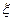 ,求
,求
 是从0,1,2,3四个数中任取一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率。
是从0,1,2,3四个数中任取一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率。 的一元
的一元 二次方程
二次方程
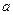 从
从 四个数中任取一个数,
四个数中任取一个数, 从
从 三个数中任取一个数,求上述方程有实根的概率。
三个数中任取一个数,求上述方程有实根的概率。 上任取一个数,
上任取一个数,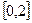 上任取一个数,求上述方程有实根的概率。
上任取一个数,求上述方程有实根的概率。 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为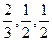 ,且各人答题正确与否相互之间没有影响.用
,且各人答题正确与否相互之间没有影响.用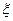 表示甲队的总得分.
表示甲队的总得分. 表示“甲、乙两个队总得分之和等于3”这一事件,用
表示“甲、乙两个队总得分之和等于3”这一事件,用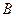 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求 .
. 各项测试合格的概率组成一个公差为
各项测试合格的概率组成一个公差为 的等差数列,且第一项测试不合格的概率超过
的等差数列,且第一项测试不合格的概率超过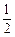 ,第一项测试不合格但第二项测试合格的概率为
,第一项测试不合格但第二项测试合格的概率为 .
. 的分布列和数学期望.
的分布列和数学期望.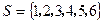 .令事件
.令事件 ,事件
,事件 ,则
,则 的值为( )
的值为( )