Question

【题目】如图所示，由直线x=a，x=a+1（a＞0），y=x2及 x 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间，即 a2＜ x2dx＜（a+1）2 ． 类比之，若对n∈N*，不等式 ＜A＜ + +…+ 恒成立，则实数A等于（ ）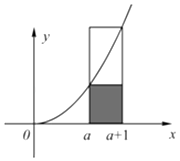
A.ln
B.ln 2
C. ln 2
D. ln 5

Answer 1

【答案】B
【解析】解：令A=A1+A2+A3+…+An ， 由题意得： ＜A1＜ ， ＜A2＜ ， ＜A3＜ ，…， ＜An＜ ，
∴A1= dx=lnx| =ln（n+1）﹣lnn，
同理：A2=﹣ln（n+1）+ln（n+2），A3=﹣ln（n+2）+ln（n+3），…，An=﹣ln（2n﹣1）+ln2n，
∴A=A1+A2+A3+…+An
=﹣lnn+ln（n+1）﹣ln（n+1）+ln（n+2）﹣ln（n+2）+ln（n+3）﹣…﹣ln（2n﹣1）+ln2n
=ln2n﹣lnn
=ln2，
故选：B．
令A=A1+A2+A3+…+An ， 根据定积分的定义得到：A1=﹣lnn+ln（n+1），同理求出A2 ， A3 ， …，An的值，相加求出即可．