题目内容
有下列命题:
①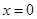 是函数
是函数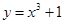 的极值点;
的极值点;
②三次函数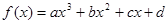 有极值点的充要条件是
有极值点的充要条件是 ;
;
③奇函数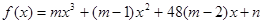 在区间
在区间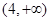 上是递增的;
上是递增的;
④曲线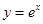 在
在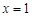 处的切线方程为
处的切线方程为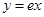 .
.
其中真命题的序号是 .
②③④
解析试题分析:对于①,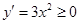 ,所以
,所以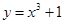 在R上单调递增,没有极值点;对于②,对于三次函数
在R上单调递增,没有极值点;对于②,对于三次函数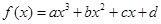 有极值点的充要条件是
有极值点的充要条件是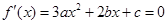 有两个不相等的实根,所以
有两个不相等的实根,所以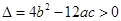 即
即 ,正确;对于③,因为函数
,正确;对于③,因为函数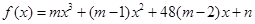 为奇函数,所以
为奇函数,所以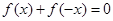 即
即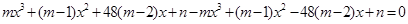 即
即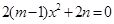 对任意
对任意 都成立,所以
都成立,所以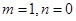 ,此时
,此时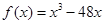 ,所以
,所以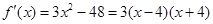 ,当
,当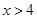 时,
时,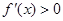 ,所以
,所以 在区间
在区间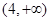 上递增;对于④,因为
上递增;对于④,因为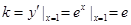 ,所以曲线
,所以曲线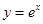 在
在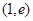 处的切线方程为
处的切线方程为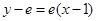 即
即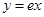 ;综上可知②③④正确.
;综上可知②③④正确.
考点:1.函数的极值与导数;2.函数的单调性与导数;3.导数的几何意义;4.充分必要条件.

练习册系列答案
相关题目
 ,
,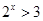 ”的否定是“
”的否定是“ ,
,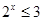 ”;②函数
”;②函数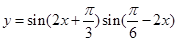 的最小正周期是
的最小正周期是 ;③命题“函数
;③命题“函数 在
在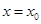 处有极值,则
处有极值,则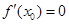 ”的否命题是真命题;④
”的否命题是真命题;④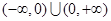 上的奇函数,
上的奇函数,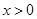 的解析式是
的解析式是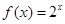 ,则
,则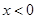 时的解析式为
时的解析式为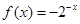 .其中正确的说法是__________.
.其中正确的说法是__________.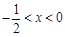 ”是“不等式
”是“不等式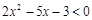 成立”的 条件(在“充分不必要”, “必要不充分”, “充要”, “既不充分又不必要”中选一个填写).
成立”的 条件(在“充分不必要”, “必要不充分”, “充要”, “既不充分又不必要”中选一个填写).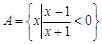 ,
,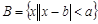 .若“a=1”是“
.若“a=1”是“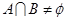 ”的充分条件, 则实数b的取值范围是 .
”的充分条件, 则实数b的取值范围是 .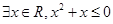 ”的否定是 .
”的否定是 . 的不等式
的不等式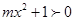 的解集是R;②函数
的解集是R;②函数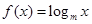 是减函数,如果这两个命题中有且只有一个是真命题,则实数的取值范围是
是减函数,如果这两个命题中有且只有一个是真命题,则实数的取值范围是  关于
关于 的不等式
的不等式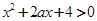 对一切
对一切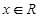 恒成立;命题
恒成立;命题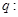 函数
函数 是减函数,若
是减函数,若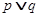 为真命题,
为真命题,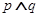 为假命题,则实数
为假命题,则实数 的取值范围为 .
的取值范围为 .