题目内容
已知单调递增的等比数列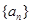 满足:
满足: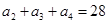 ,且
,且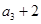 是
是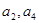 的等差中项.
的等差中项.
(1)求数列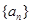 的通项公式;
的通项公式;
(2)若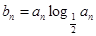 ,
,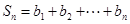 ,求使
,求使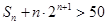 成立的正整数
成立的正整数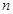 的最小值.
的最小值.
【答案】
(1)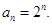 ;(2)5
;(2)5
【解析】
试题分析:(1)由等差中项得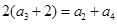 ,再联立
,再联立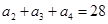 列方程并结合等比数列的单调性求
列方程并结合等比数列的单调性求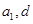 ,进而根据等比数列的通项公式求
,进而根据等比数列的通项公式求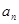 ;(2)求数列的前n项和,首先考虑其通项公式,根据通项公式特点来选择适合的求和方法,该题由(1)得
;(2)求数列的前n项和,首先考虑其通项公式,根据通项公式特点来选择适合的求和方法,该题由(1)得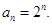 ,代入
,代入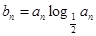 中,可求得
中,可求得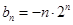 ,故可采取错位相减法求
,故可采取错位相减法求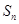 ,然后代入不等式
,然后代入不等式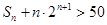 中,得关于n的不等式,进而考虑其不等式解即可.
中,得关于n的不等式,进而考虑其不等式解即可.
试题解析:(1)设等比数列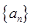 的首项为
的首项为 ,公比为
,公比为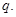 依题意,有
依题意,有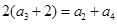 ,代入
,代入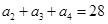 ,得
,得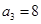 ,
,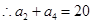 ,
,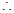
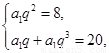 解之得
解之得 或
或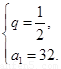
又数列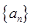 单调递增,所以
单调递增,所以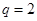 ,
,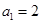 ,
, 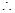 数列
数列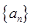 的通项公式为
的通项公式为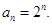
(2)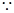
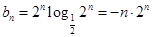 ,
,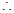
 ,
,
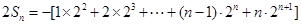 ,
,
两式相减,得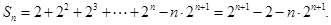
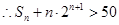 即
即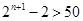 ,即
,即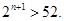
易知:当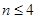 时,
时, ,当
,当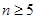 时,
时,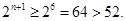
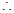 使
使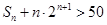 成立的正整数
成立的正整数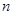 的最小值为5.
的最小值为5.
考点:1、等差中项;2、等比数列的通项公式;3、数列求和.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目