题目内容
(2007•武汉模拟)已知单调递增的等比数列{an}中,a2+a3+a4=28,且a3+2是a2、a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=log2an,求数列{
}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)若bn=log2an,求数列{
| 1 | bnbn+1 |
分析:(1)由
及a2•a4=
,可求a2,a4,结合a1=2,可求q,进而可求an
(2)由(1)可得bn=n.
=
=
-
,考虑利用裂项求和即可
|
| a | 2 3 |
(2)由(1)可得bn=n.
| 1 |
| bnbn+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:解:(1)由
及a2•a4=
,
解得
或
(a2>a4不合题意,舍去).(4分)
从而a1=2,q=2.∴an=2n(6分)
(2)∵bn=log22n=n.(8分)
=(1-
)+(
-
)+…+(
-
)=1-
=
.(12分)
|
| a | 2 3 |
解得
|
|
从而a1=2,q=2.∴an=2n(6分)
(2)∵bn=log22n=n.(8分)
|
=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题主要考查 了利用登比数列基本量求解数列的通项公式,数列求和的裂项求和的应用,属于基本方法的简单应用.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
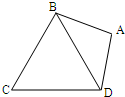 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=