题目内容
直线y=a与函数f(x)=x3-3x的图象有相异的三个交点,求a的取值范围.
分析:∵y=a与f(x)=x3-3x的图象有相异的三个交点,知f(x)=x3-3x有两个“拐点”(已具备),且两“拐点”分布在y=a的两侧,即有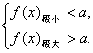 故需求f(x)的极值.
故需求f(x)的极值.
解:研究函数y=a与函数f(x)=x3-3x的交点个数,由于y=a是一条平行于x轴(a=0时与x轴重合)的直线,
∴只需研究函数f(x)=x3-3x图象的变化趋势即可.
∵f′(x)=3x2-3=3(x-1)(x+1),∴在区间(-∞,-1]上,f(x)递增;
在[-1,1]上,f(x)递减;
在[1,+∞)上,f(x)递增.
∴[f(x)]极小值=-2,[f(x)]极大值=2.
因此,要使y=a与函数f(x)的图象有相异的三个交点,必须有a∈(-2,2).

练习册系列答案
相关题目