题目内容
16、直线y=a与函数f（x）=x3-3x的图象有三个互不相同的公共点，求a的取值范围．
分析：首先根据函数的导数求出函数的单调区间，然后画出函数的图象，从而根据图象判断函数与直线的公共点的情况．
解答：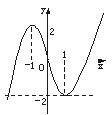
解：先求函数f（x）的单调区间，
由f′（x）=3x2-3=0，
解得x=±1，
当x＜-1或x＞1时，f′（x）＞0，
当-1＜x＜1时，f′（x）＜0，
∴在（-∞，-1）和（1，+∞）上，f（x）=x3-3x是增函数，
在（-1，1）上，f（x）=x3-3x是减函数，
由此可以作出f（x）=x3-3x的草图（如图）．
由图可知，当且仅当-2＜a＜2时，
直线y=a与函数f（x）=x3-3x的图象有三个互不相同的公共点．
解：先求函数f（x）的单调区间，由f′（x）=3x2-3=0，
解得x=±1，
当x＜-1或x＞1时，f′（x）＞0，
当-1＜x＜1时，f′（x）＜0，
∴在（-∞，-1）和（1，+∞）上，f（x）=x3-3x是增函数，
在（-1，1）上，f（x）=x3-3x是减函数，
由此可以作出f（x）=x3-3x的草图（如图）．
由图可知，当且仅当-2＜a＜2时，
直线y=a与函数f（x）=x3-3x的图象有三个互不相同的公共点．
点评：掌握由导数求函数单调性的方法．
练习册系列答案
相关题目