题目内容
已知点(n,an)(n∈N*)在函数f(x)=-6x-2的图象上,数列{an}的前n项和为Sn.
(Ⅰ)求Sn;
(Ⅱ)设cn=an+8n+3,数列{dn}满足d1=c1,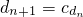 (n∈N*).求数列{dn}的通项公式;
(n∈N*).求数列{dn}的通项公式;
(Ⅲ)设g(x)是定义在正整数集上的函数,对于任意的正整数x1、x2,恒有g(x1x2)=x1g(x2)+x2g(x1)成立,且g(2)=a(a为常数,且a≠0),记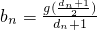 ,试判断数列{bn}是否为等差数列,并说明理由.
,试判断数列{bn}是否为等差数列,并说明理由.
解:(Ⅰ)由已知an=-6n-2,故{an}是以a1=-8为首项公差为-6的等差数列.
所以Sn=-3n2-5n.
(Ⅱ)因为cn=an+8n+3=-6n-2+8n+3=2n+1(n∈N*),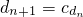 =2dn+1,因此dn+1+1=2(dn+1)(n∈N*).
=2dn+1,因此dn+1+1=2(dn+1)(n∈N*).
由于d1=c1=3,
所以{dn+1}是首项为d1+1=4,公比为2的等比数列.
故dn+1=4×2n-1=2n+1,所以dn=2n+1-1.
(Ⅲ)解法一: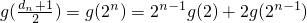 ,
,
则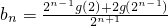 =
= +
+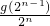 ,bn+1=
,bn+1= +
+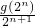 .
.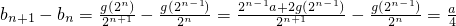 .
.
因为a为常数,则数列{bn}是等差数列.
解法二:因为g(x1x2)=x1g(x2)+x2g(x1)成立,且g(2)=a,
故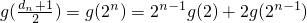 =2n-1g(2)+2[2n-2g(2)+2g(2n-2)]=2×2n-1g(2)+22g(2n-2)=2×2n-1g(2)+22[2n-3g(2)+2g(2n-3)]=3×2n-1g(2)+23g(2n-3)═(n-1)×2n-1g(2)+2n-1g(2)=n•2n-1g(2)=an•2n-1,
=2n-1g(2)+2[2n-2g(2)+2g(2n-2)]=2×2n-1g(2)+22g(2n-2)=2×2n-1g(2)+22[2n-3g(2)+2g(2n-3)]=3×2n-1g(2)+23g(2n-3)═(n-1)×2n-1g(2)+2n-1g(2)=n•2n-1g(2)=an•2n-1,
所以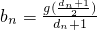 =
=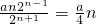 .
.
则 .
.
由已知a为常数,因此,数列{bn}是等差数列.
分析:(Ⅰ)由题意可知{an}是以a1=-8为首项公差为-6的等差数列.由此可以求得Sn=-3n2-5n.
(Ⅱ)由cn=an+8n+3=-6n-2+8n+3=2n+1(n∈N*),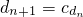 =2dn+1,可知dn+1+1=2(dn+1)(n∈N*).再由d1=c1=3,可知{dn+1}是首项为d1+1=4,公比为2的等比数列.由此能够求得dn=2n+1-1.
=2dn+1,可知dn+1+1=2(dn+1)(n∈N*).再由d1=c1=3,可知{dn+1}是首项为d1+1=4,公比为2的等比数列.由此能够求得dn=2n+1-1.
(Ⅲ)解法一:由题意可知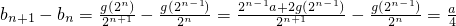 .由此可知数列{bn}是等差数列.
.由此可知数列{bn}是等差数列.
解法二:因为g(x1x2)=x1g(x2)+x2g(x1)成立,且g(2)=a,故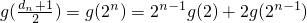 =an•2n-1,由此可知
=an•2n-1,由此可知 .因此,数列{bn}是等差数列.
.因此,数列{bn}是等差数列.
点评:本题考查数列的性质及其综合运用,具有一定的难度,解题时认真审题,仔细解答.
所以Sn=-3n2-5n.
(Ⅱ)因为cn=an+8n+3=-6n-2+8n+3=2n+1(n∈N*),
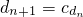 =2dn+1,因此dn+1+1=2(dn+1)(n∈N*).
=2dn+1,因此dn+1+1=2(dn+1)(n∈N*).由于d1=c1=3,
所以{dn+1}是首项为d1+1=4,公比为2的等比数列.
故dn+1=4×2n-1=2n+1,所以dn=2n+1-1.
(Ⅲ)解法一:
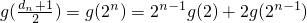 ,
,则
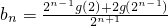 =
= +
+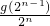 ,bn+1=
,bn+1= +
+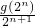 .
.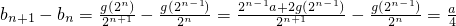 .
.因为a为常数,则数列{bn}是等差数列.
解法二:因为g(x1x2)=x1g(x2)+x2g(x1)成立,且g(2)=a,
故
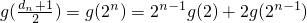 =2n-1g(2)+2[2n-2g(2)+2g(2n-2)]=2×2n-1g(2)+22g(2n-2)=2×2n-1g(2)+22[2n-3g(2)+2g(2n-3)]=3×2n-1g(2)+23g(2n-3)═(n-1)×2n-1g(2)+2n-1g(2)=n•2n-1g(2)=an•2n-1,
=2n-1g(2)+2[2n-2g(2)+2g(2n-2)]=2×2n-1g(2)+22g(2n-2)=2×2n-1g(2)+22[2n-3g(2)+2g(2n-3)]=3×2n-1g(2)+23g(2n-3)═(n-1)×2n-1g(2)+2n-1g(2)=n•2n-1g(2)=an•2n-1,所以
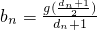 =
=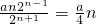 .
.则
 .
.由已知a为常数,因此,数列{bn}是等差数列.
分析:(Ⅰ)由题意可知{an}是以a1=-8为首项公差为-6的等差数列.由此可以求得Sn=-3n2-5n.
(Ⅱ)由cn=an+8n+3=-6n-2+8n+3=2n+1(n∈N*),
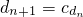 =2dn+1,可知dn+1+1=2(dn+1)(n∈N*).再由d1=c1=3,可知{dn+1}是首项为d1+1=4,公比为2的等比数列.由此能够求得dn=2n+1-1.
=2dn+1,可知dn+1+1=2(dn+1)(n∈N*).再由d1=c1=3,可知{dn+1}是首项为d1+1=4,公比为2的等比数列.由此能够求得dn=2n+1-1.(Ⅲ)解法一:由题意可知
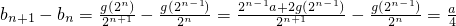 .由此可知数列{bn}是等差数列.
.由此可知数列{bn}是等差数列.解法二:因为g(x1x2)=x1g(x2)+x2g(x1)成立,且g(2)=a,故
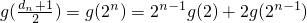 =an•2n-1,由此可知
=an•2n-1,由此可知 .因此,数列{bn}是等差数列.
.因此,数列{bn}是等差数列.点评:本题考查数列的性质及其综合运用,具有一定的难度,解题时认真审题,仔细解答.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目