题目内容
直线l1过(1,0)点,且l1关于直线y=x对称直线为l2,已知点A(n,
)(n∈N+)在l2上,a1=1,当n≥2时,an+1an-1=anan-1+an2.
(Ⅰ)求l2的方程;
(Ⅱ)求{an}的通项公式.
| an+1 | an |
(Ⅰ)求l2的方程;
(Ⅱ)求{an}的通项公式.
分析:(Ⅰ)设l2的方程为:y=kx+b,,由l1,l2关于直线y=x对称,及l1过点(1,0)可得l2过点(0,1),可求b
再由An (n,
)在直线l2上,可得
=k+1,
=2k+1,k=
-
.及
-
=1可求k
(Ⅱ)由
-
=1,可知{
}是首项为
,公差为1的等差数列.从而可得
=2+(n-1)×1=n+1,利用叠乘法可求
再由An (n,
| an+1 |
| an |
| a2 |
| a1 |
| a3 |
| a2 |
| a3 |
| a2 |
| a2 |
| a1 |
| an+1 |
| an |
| an |
| an-1 |
(Ⅱ)由
| an+1 |
| an |
| an |
| an-1 |
| an+1 |
| an |
| a2 |
| a1 |
| an+1 |
| an |
解答:解:(Ⅰ)设l2的方程为:y=kx+b,
又l1,l2关于直线y=x对称,l1过点(1,0),∴l2过点(0,1),∴b=1.
又∵An (n,
)在直线l2上,取n=1,2得:
=k+1,
=2k+1,∴k=
-
.
∵an+1an-1=anan-1+an2,∴
-
=1(n∈N,n≥2),
∴k=
-
=1,∴l2的方程为y=x+1.
(Ⅱ)由
-
=1,可知{
}是首项为
,公差为1的等差数列.
∵A1(1,
)在直线l2上,∴
=2.∴
=2+(n-1)×1=n+1,
∴an=
×
×…×
×a1=n×(n-1)×…×2×1=n!
又l1,l2关于直线y=x对称,l1过点(1,0),∴l2过点(0,1),∴b=1.
又∵An (n,
| an+1 |
| an |
| a2 |
| a1 |
| a3 |
| a2 |
| a3 |
| a2 |
| a2 |
| a1 |
∵an+1an-1=anan-1+an2,∴
| an+1 |
| an |
| an |
| an-1 |
∴k=
| a3 |
| a2 |
| a2 |
| a1 |
(Ⅱ)由
| an+1 |
| an |
| an |
| an-1 |
| an+1 |
| an |
| a2 |
| a1 |
∵A1(1,
| a2 |
| a1 |
| a2 |
| a1 |
| an+1 |
| an |
∴an=
| an |
| an-1 |
| an-1 |
| an-2 |
| a2 |
| a1 |
点评:本题主要考查了利用构造法求解数列的通项公式,数列的叠乘求解数列的通项公式,叠加与叠乘法的求解中要注意所写的式子的个数的判断是解题中的易错点

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
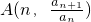 (n∈N+)在l2上,a1=1,当n≥2时,an+1an-1=anan-1+an2.
(n∈N+)在l2上,a1=1,当n≥2时,an+1an-1=anan-1+an2.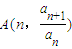 (n∈N+)在l2上,a1=1,当n≥2时,an+1an-1=anan-1+an2.
(n∈N+)在l2上,a1=1,当n≥2时,an+1an-1=anan-1+an2.