题目内容
【题目】已知两个函数f(x)=log4(a ![]() )(a≠0),g(x)=log4(4x+1)﹣
)(a≠0),g(x)=log4(4x+1)﹣ ![]() 的图象有且只有一个公共点,则实数a的取值范围是 .
的图象有且只有一个公共点,则实数a的取值范围是 .
【答案】{a,a>1或a=﹣3}
【解析】g(x)=log4(a2x﹣ ![]() a),
a),
函数f(x)与g(x)的图象有且只有一个公共点,即
方程f(x)=g(x)只有一个解
由已知得log4(4x+1) ![]() x=log4(a2x﹣
x=log4(a2x﹣ ![]() a),
a),
∴log4( ![]() )=log4(a2x﹣
)=log4(a2x﹣ ![]() a),
a),
方程等价于 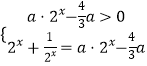 ,
,
设2x=t,t>0,则(a﹣1)t2﹣ ![]() at﹣1=0有一解
at﹣1=0有一解
若a﹣1>0,设h(t)=(a﹣1)t2﹣ ![]() at﹣1,
at﹣1,
∵h(0)=﹣1<0,∴恰好有一正解
∴a>1满足题意
若a﹣1=0,即a=1时,h(t)=﹣ ![]() ﹣1,由h(t)=0,得t=﹣
﹣1,由h(t)=0,得t=﹣ ![]() <0,不满足题意
<0,不满足题意
若a﹣1<0,即a<1时,由△=(﹣ ![]() )2﹣4(a﹣1)×(﹣1)=0,得a=﹣3或a=
)2﹣4(a﹣1)×(﹣1)=0,得a=﹣3或a= ![]() ,
,
当a=﹣3时,t= ![]() 满足题意
满足题意
当a= ![]() 时,t=﹣2(舍去)
时,t=﹣2(舍去)
综上所述实数a的取值范围是{a|a>1或a=﹣3}.
所以答案是:{a|a>1或a=﹣3}.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目