题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,点E是棱PA的中点,PB=PD,平面BDE⊥平面ABCD. 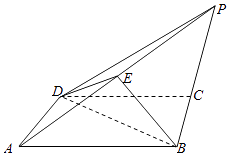
(Ⅰ)求证:PC∥平面BDE;
(Ⅱ)求证:PC⊥平面ABCD;
(Ⅲ)设PC=λAB,试判断平面PAD⊥平面PAB能否成立;若成立,写出λ的一个值(只需写出结论).
【答案】证明:(Ⅰ)设AC∩BD=O,连接OE,
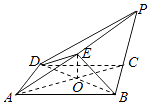
因为底面ABCD为正方形,所以O是AC的中点,又点E是棱PA的中点,
所以EO是的△PAC中位线,所以EO∥PC
因为EO平面BDE,PC平面BDE,
所以PC∥平面BDE.
(Ⅱ)证法一:在△PAB和△PAD中,
因为AB=AD,PB=PD,PA=PA,
所以△PAB≌△PAD,又点E是棱PA的中点,
所以EB=ED,所以EO⊥BD,
因为平面BDE⊥平面ABCD,平面BDE∩平面ABCD=BD,EO平面BDE
所以EO⊥平面ABCD,所以EO⊥AC,EO⊥BD,
因为EO∥PC,所以PC⊥AC,PC⊥BD,又AC∩BD=O
所以PC⊥平面ABCD.
证法二:连接PO,

因为底面ABCD是正方形,
所以O是BD的中点,BD⊥AC,又PB=PD,所以PO⊥BD,
又PO∩AC=O,PO平面PAC,AC平面PAC
所以BD⊥平面PAC
又OE平面PAC,所以BD⊥OE,
因为平面BDE⊥平面ABCD,平面BDE∩平面ABCD=BD,EO平面BDE
所以EO⊥平面ABCD,所以EO⊥AC,EO⊥BD,
因为OE∥PC,所以PC⊥AC,PC⊥BD,又AC∩BD=O
所以PC⊥平面ABCD.
(Ⅲ)不能成立.
【解析】(Ⅰ)设AC∩BD=O,连接OE,推导出EO∥PC,由此能证明PC∥平面BDE.(Ⅱ)法一:推导出△PAB≌△PAD,EO⊥BD,从而EO⊥平面ABCD,进而EO⊥AC,EO⊥BD,由此得到PC⊥AC,PC⊥BD,从而能证明PC⊥平面ABCD.
法二:连接PO,推导出BD⊥AC,PO⊥BD,从而BD⊥平面PAC,进而BD⊥OE,由此得到EO⊥平面ABCD,从而EO⊥AC,EO⊥BD,进而PC⊥AC,PC⊥BD,由此能证明PC⊥平面ABCD.(Ⅲ)由PC=λAB,得到平面PAD⊥平面PAB不能成立.
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】如表是某校120名学生假期阅读时间(单位:小时)的频率分布表,现用分层抽样的方法从[10,15),[15,20),[20,25),[25,30)四组中抽取20名学生了解其阅读内容,那么从这四组中依次抽取的人数是( )
分组 | 频数 | 频率 |
[10,15) | 12 | 0,10 |
[15,20) | 30 | a |
[20,25) | m | 0.40 |
[25,30) | n | 0.25 |
合计 | 120 | 1.00 |
A.2,5,8,5
B.2,5,9,4
C.4,10,4,2
D.4,10,3,3

