题目内容
【题目】已知函数
.
（1）若
只有一个零点，求
；
（2）当
时，对任意
，
恒成立，求的取值范围．
【答案】（1）
．（2）
【解析】
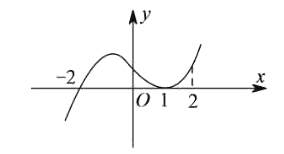
(1)利用导函数研究原函数的单调性得函数的大致图象，解决零点问题；
(2)从表象看是双变量的问题，实质可转化为求闭区间上的最值问题.
解：（1）函数
的定义域为
，
，
当
时，
，
，所以在
上单调递减；
，
，所以在
上单调递增，
所以
，
故此时函数没有零点．
当
时，，，所以在上单调递减；
，，所以在上单调递增，
所以
，
因为函数只有一个零点，所以
，即．
（2）因为
，所以
．
由（1）知在
上单调递减，在
上单调递增，所以．
因为
与
，所以
，
设
，
则
，
所以
在上单调递增，故
，所以
，
从而
，
所以
，即
．
设
，则
．
当时，
，所以
在上单调递增，
又
，所以，等价于
，则．
因为，所以
的取值范围为．
练习册系列答案
阅读快车系列答案
相关题目
【题目】如今我们的互联网生活日益丰富，除了可以很方便地网购，网上叫外卖也开始成为不少人日常生活中不可或缺的一部分，为了解网络外卖在
市的普及情况， 
市某调查机构借助网络进行了关于网络外卖的问卷调查，并从参与调查的网民中抽取了200人进行抽样分析，得到表格（单位：人）.
（1）根据表中数据，能否在犯错误的概率不超过0.15的前提下认为
市使用网络外卖的情况与性别有关？
（2）①现从所抽取的女网民中利用分层抽样的方法再抽取5人，再从这5人中随机选出了3人赠送外卖优惠券，求选出的3人中至少有2人经常使用网络外卖的概率；
②将频率视为概率，从
市所有参与调查的网民中随机抽取10人赠送礼品，记其中经常使用网络外卖的人数为
，求
的数学期望和方差.
参考公式： 
，其中
.
参考数据：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
