题目内容
已知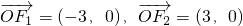 ,为坐标原点,动点M满足
,为坐标原点,动点M满足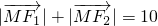 .
.
(1)求动点M的轨迹C;
(2)若点P、Q是曲线C上的任意两点,且 ,求
,求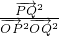 的值.
的值.
解:(1)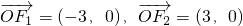 ,
,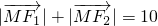 >6.
>6.
∴动点M的轨迹C是焦点在x轴,c=3,a=5的椭圆,
∴动点M的轨迹C的轨迹方程是 .
.
(2)由题意可知,取Q(0,4),P(5,0),则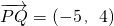 ,
,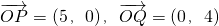 ,
,
∴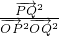 =
=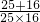 =
=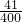 .
.
分析:(1)∵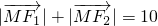 >6,∴动点M的轨迹C是焦点在x轴,c=3,a=5的椭圆.
>6,∴动点M的轨迹C是焦点在x轴,c=3,a=5的椭圆.
(2)采用特殊值法,设P(m,m),Q(-m,m),能够快速求解.
点评:本题考查椭圆的性质及应用,解题时注意特殊值法的运用,能够简化运用.
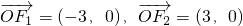 ,
,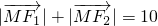 >6.
>6.∴动点M的轨迹C是焦点在x轴,c=3,a=5的椭圆,
∴动点M的轨迹C的轨迹方程是
 .
.(2)由题意可知,取Q(0,4),P(5,0),则
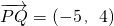 ,
,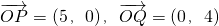 ,
,∴
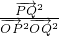 =
=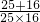 =
=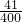 .
.分析:(1)∵
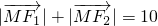 >6,∴动点M的轨迹C是焦点在x轴,c=3,a=5的椭圆.
>6,∴动点M的轨迹C是焦点在x轴,c=3,a=5的椭圆.(2)采用特殊值法,设P(m,m),Q(-m,m),能够快速求解.
点评:本题考查椭圆的性质及应用,解题时注意特殊值法的运用,能够简化运用.

练习册系列答案
相关题目
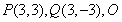
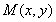

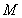
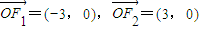 ,为坐标原点,动点M满足
,为坐标原点,动点M满足 .
.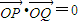 ,求
,求 的值.
的值.