题目内容
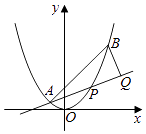
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
【答案】
(1)
解:(1)∵y2=2px过点P(1,1),
∴1=2p,
解得p= ![]() ,
,
∴y2=x,
∴焦点坐标为( ![]() ,0),准线为x=﹣
,0),准线为x=﹣ ![]() ,
,
(2)
(2)证明:设过点(0, ![]() )的直线方程为
)的直线方程为
y=kx+ ![]() ,M(x1,y1),N(x2,y2),
,M(x1,y1),N(x2,y2),
∴直线OP为y=x,直线ON为:y= ![]() x,
x,
由题意知A(x1,x1),B(x1, ![]() ),
),
由  ,可得k2x2+(k﹣1)x+
,可得k2x2+(k﹣1)x+ ![]() =0,
=0,
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]()
∴y1+ ![]() =kx1+
=kx1+ ![]() +
+ ![]() =2kx1+
=2kx1+ ![]() =2kx1+
=2kx1+  =
= ![]()
∴A为线段BM的中点.

【解析】(1.)根据抛物线过点P(1,1).代值求出p,即可求出抛物线C的方程,焦点坐标和准线方程;
(2.)设过点(0, ![]() )的直线方程为y=kx+
)的直线方程为y=kx+ ![]() ,M(x1 , y1),N(x2 , y2),根据韦达定理得到x1+x2=
,M(x1 , y1),N(x2 , y2),根据韦达定理得到x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,根据中点的定义即可证明.
,根据中点的定义即可证明.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目