题目内容
【题目】米勒问题,是指德国数学家米勒1471年向诺德尔教授提出的有趣问题:在地球表面的什么部位,一根垂直的悬杆呈现最长(即可见角最大?)米勒问题的数学模型如下:如图,设![]() 是锐角
是锐角![]() 的一边
的一边![]() 上的两定点,点
上的两定点,点![]() 是边
是边![]() 边上的一动点,则当且仅当
边上的一动点,则当且仅当![]() 的外接圆与边
的外接圆与边![]() 相切时,
相切时,![]() 最大.若
最大.若![]() ,点
,点![]() 在
在![]() 轴上,则当
轴上,则当![]() 最大时,点
最大时,点![]() 的坐标为( )
的坐标为( )
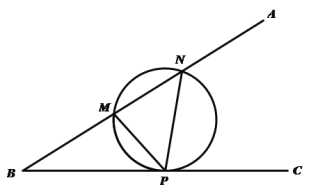
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】A
【解析】
设点![]() 的坐标为
的坐标为![]() ,求出线段
,求出线段![]() 的中垂线与线段
的中垂线与线段![]() 的中垂线交点的横坐标,即可得到
的中垂线交点的横坐标,即可得到![]() 的外接圆圆心的横坐标,由
的外接圆圆心的横坐标,由![]() 的外接圆与边
的外接圆与边![]() 相切于点
相切于点![]() ,可知
,可知![]() 的外接圆圆心的横坐标与点
的外接圆圆心的横坐标与点![]() 的横坐标相等,即可得到点
的横坐标相等,即可得到点![]() 的坐标。
的坐标。
由于点![]() 是边
是边![]() 边上的一动点,且点
边上的一动点,且点![]() 在
在![]() 轴上,故设点
轴上,故设点![]() 的坐标为
的坐标为![]() ;
;
由于![]() ,则直线
,则直线![]() 的方程为:
的方程为:![]() ,点
,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,故点
轴的交点,故点![]() 的坐标为
的坐标为![]() ;由于
;由于![]() 为锐角,点
为锐角,点![]() 是边
是边![]() 边上的一动点,故
边上的一动点,故![]() ;
;
所以线段![]() 的中垂线
的中垂线![]() 方程为:
方程为:![]() ;线段
;线段![]() 的中垂线
的中垂线![]() 方程为:
方程为:![]() ;
;
故![]() 的外接圆的圆心为直线
的外接圆的圆心为直线![]() 与直线
与直线![]() 的交点,联立
的交点,联立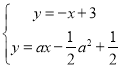 ,解得:
,解得:![]() ;即
;即![]() 的外接圆圆心的横坐标为
的外接圆圆心的横坐标为![]()
![]()
![]() 的外接圆与边
的外接圆与边![]() 相切于点
相切于点![]() ,边
,边![]() 在
在![]() 轴上,则
轴上,则![]() 的外接圆圆心的横坐标与点
的外接圆圆心的横坐标与点![]() 的横坐标相等,即
的横坐标相等,即![]() ,解得:
,解得:![]() 或
或![]() (舍)
(舍)
所以点![]() 的坐标为
的坐标为![]() ;
;
故答案选A

练习册系列答案
相关题目
